Endomorphisme

[Aury41]

Bonjour,
Je suis bloqué sur un exercice et j'aurai besoin d'aide
Voici le sujet:
Soit E un K-espace vectoriel de dimension 4 et f un endomorphisme de E.
On suppose qu’il existe u, v ∈ E tels que β := (u, v, f(u), f(v)) soit une base de E et qu’il existe α1, α2 ∈ K tels que
u + α1f(u) + α2f^2(u) = 0, v + α1f(v) + α2f^2(v) = 0.
1. Vérifier que α2 ≠ 0.
2. Déterminer la matrice A de f relativement à la base β. En déduire son rang.
3. Montrer qu’il existe γ1, γ2 ∈ K tels que γ1f^2 + γ2f + idE = 0

Merci d'avance pour votre aide

[GaBuZoMeu]

Bonsoir,
Qu'as-u essayé pour montrer que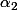 est non nul ? À ta place je supposerais que 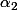est nul et j'essaierais d'en déduire quelque chose contradictoire avec les hypôthèses.