Bonjour,
Comment savoir à partir de quel rang, n (e Z) satisfait l'inégalité 4^n > 4n+1 ?
Je vous remercie d'avance.
Comparaison suite arithmétique / géométrique
5 messages
- Page 1 sur 1
Re: Comparaison suite arithmétique / géométrique
Bonsoir
n<0 , tous, clairement
n=0 , n=1 , non
n=2 oui
puis par récurrence pour n> ou = 2
Proposez vos essais ...
n<0 , tous, clairement
n=0 , n=1 , non
n=2 oui
puis par récurrence pour n> ou = 2
Proposez vos essais ...
Re: Comparaison suite arithmétique / géométrique
bonsoir,
concernant
pose comme hypothèse de récurrence H_n:

puis multiplie les deux membres par 4.

à droite, on trouve que l'on peut comparer avec
que l'on peut comparer avec +1=4n+5)
On trouve que la propriété H_n est héréditaire dès que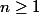
concernant
pose comme hypothèse de récurrence H_n:
puis multiplie les deux membres par 4.
à droite, on trouve
On trouve que la propriété H_n est héréditaire dès que
Re: Comparaison suite arithmétique / géométrique
Ben...c'est ce que j'attendais de julienboleee..
Conformément aux principes du forum
Conformément aux principes du forum
Re: Comparaison suite arithmétique / géométrique
Bonsoir mathelot
la propriété est héréditaire à partir de 0 car p(0)=F et donc p(0)impliquep(1) =V ...
la propriété est héréditaire à partir de 0 car p(0)=F et donc p(0)impliquep(1) =V ...
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
