Bonjour,
Je bloque sur la résolution d'une énigme,
il s'agit de calculer la limite en +infini du produit :
(9/10) x (99/100) x (999/1000) ...... ((10^n-1)/10^n)
Si cela peut aider pour trouver une méthode, la valeur tend vraisemblablement vers 8 / 9
Limite d'un produit (10^n-1)/10^n
10 messages
- Page 1 sur 1
Re: limite d'un produit (10^n-1)/10^n
Bonjour
En prenant le ln
Ensuite=ln(1-\frac{1}{10^n})\sim-\frac{1}{10^n})
En faire la somme et la limite de la somme etc...
En prenant le ln
Ensuite
En faire la somme et la limite de la somme etc...
Re: limite d'un produit (10^n-1)/10^n
J'ai des gros doutes avec le résultat  9
9
 9=0.888888889
9=0.888888889
Et on est plutôt vers du 0.8900101
Si tu es à l'aise avec les logarithmes, c'est certainement une bonne piste pour cette énigme.
 = le n-ième terme
= le n-ième terme
=) une somme.
une somme.
Les premiers termes de cette somme sont calculables.
Pour les termes suivants,) peut être encadré de façon assez précise.
peut être encadré de façon assez précise.
Et tu te retrouves avec des sommes de suites géométriques, faciles à calculer.
... comme catamat
 9
9  9=0.888888889
9=0.888888889Et on est plutôt vers du 0.8900101
Si tu es à l'aise avec les logarithmes, c'est certainement une bonne piste pour cette énigme.
Les premiers termes de cette somme sont calculables.
Pour les termes suivants,
Et tu te retrouves avec des sommes de suites géométriques, faciles à calculer.
... comme catamat
Re: limite d'un produit (10^n-1)/10^n
Merci pour les réponses
Non je ne suis vraiment pas à l'aise avec les logarithmes... c'est pourquoi j'appelais à l'aide ici. (et je crois qu'il faudra m'en dire un peu plus).
Non je ne suis vraiment pas à l'aise avec les logarithmes... c'est pourquoi j'appelais à l'aide ici. (et je crois qu'il faudra m'en dire un peu plus).
Re: limite d'un produit (10^n-1)/10^n
Le logarithme, c'est un truc magique qui permet de dire : je n'aime pas les multiplications, je préfère les additions. Donc, plutôt que faire des multiplications, je vais faire des additions... et je ùe débrouillerai pour trouver le résultat comme ça.
La formule magique, c'est que = ln(a)+ln(b))
et en généralisant : = ln(a)+ln(b) + ln(c) + ... + ln(z))
Quand on a calculé+ln(b) + ln(c) + ... + ln(z)) , ça ne nous donne pas directement le produit qu'on cherchait. il faut utiliser la fonction exponentielle pour retrouver le résultat cherché.
, ça ne nous donne pas directement le produit qu'on cherchait. il faut utiliser la fonction exponentielle pour retrouver le résultat cherché.
Ici, le nombre que tu cherches est environ 0.8900101
La formule magique, c'est que
et en généralisant :
Quand on a calculé
Ici, le nombre que tu cherches est environ 0.8900101
Re: limite d'un produit (10^n-1)/10^n
Merci pour toutes ces précisions, que j'avais en gros.
Ce que je ne parviens pas à faire, c'est à trouver LA réponse à la question posée.
Si je fais faire le calcul en programmant, je trouve effectivement grosso modo les 0,8900101, mais le calcul est très vite limité par la puissance de calcul des programmes.
Et je ne suis pas certain que l'on ne soir pas là devant une solution fonction de (n) qui diminue extrêmement lentement pour terminer aux 8 / 9 évoqués. C'est pourquoi calculer un nombre qui soit ''environ'' ne me convient pas.
J'ai trouvé la démonstration pour la limite de 9/10 x 19/20 x 29/30 x ... (10n-1)/10n (sans utiliser les logarithmes). Si j'évoque cette autre suite, c'est parce que tout essai de calcul informatique de celle-ci donne un nombre TRES différent de la vraie limite.
Je pense que mon problème avec les (10^n-1)/10^n est de même nature, et j'espère qu'une démonstration du calcul de la limite est possible...
Ce que je ne parviens pas à faire, c'est à trouver LA réponse à la question posée.
Si je fais faire le calcul en programmant, je trouve effectivement grosso modo les 0,8900101, mais le calcul est très vite limité par la puissance de calcul des programmes.
Et je ne suis pas certain que l'on ne soir pas là devant une solution fonction de (n) qui diminue extrêmement lentement pour terminer aux 8 / 9 évoqués. C'est pourquoi calculer un nombre qui soit ''environ'' ne me convient pas.
J'ai trouvé la démonstration pour la limite de 9/10 x 19/20 x 29/30 x ... (10n-1)/10n (sans utiliser les logarithmes). Si j'évoque cette autre suite, c'est parce que tout essai de calcul informatique de celle-ci donne un nombre TRES différent de la vraie limite.
Je pense que mon problème avec les (10^n-1)/10^n est de même nature, et j'espère qu'une démonstration du calcul de la limite est possible...
Re: limite d'un produit (10^n-1)/10^n
Je définis différentes suites :
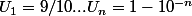
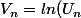)
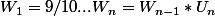 : la suite qui nous intéresse
: la suite qui nous intéresse
Prenons les 10 premiers termes de U_n, ou encore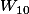 :
:
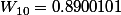
Est-ce que la suite va descendre beaucoup plus bas ?
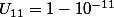
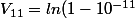)
Pour des nombres comme ça, très proches de 1, on sait faire un encadrement de ln (1+h) (avec h petit)
 < h)
La somme de tous les) est comprise entre la somme des
est comprise entre la somme des 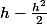 et la somme des
et la somme des 
On a des sommes de suites géométriques, ce sont des sommes faciles à calculer.
Somme des termes d'une suite géométrique = (1er terme pris moins premier terme non-pris), divisé par 1 moins la raison.
Somme 1=
Somme 2 =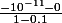
La somme de tous les logarithmes , à partir du 11 ème terme, c'est donc un nombre proche de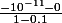 ; c'est uniquement à partir de la 22ème décimale qu'on a des écarts.
; c'est uniquement à partir de la 22ème décimale qu'on a des écarts.
Quand on calcule l'exponentielle d'un nombre très très proche de 1, comme c'est le cas ici, ça revient à ajouter 1 ; là encore, c'est à partir de la 22ème décimale qu'on peut avoir des différences.
Quand on a trouvé le produit des 10 premiers termes, pour trouver la solution avec l'infinité de termes, on va donc multiplier par un nombre proche de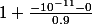 ... avec des différences à partir de la 22ème décimale.
... avec des différences à partir de la 22ème décimale.
Prenons les 10 premiers termes de U_n, ou encore
Est-ce que la suite va descendre beaucoup plus bas ?
Pour des nombres comme ça, très proches de 1, on sait faire un encadrement de ln (1+h) (avec h petit)
La somme de tous les
On a des sommes de suites géométriques, ce sont des sommes faciles à calculer.
Somme des termes d'une suite géométrique = (1er terme pris moins premier terme non-pris), divisé par 1 moins la raison.
Somme 1=
Somme 2 =
La somme de tous les logarithmes , à partir du 11 ème terme, c'est donc un nombre proche de
Quand on calcule l'exponentielle d'un nombre très très proche de 1, comme c'est le cas ici, ça revient à ajouter 1 ; là encore, c'est à partir de la 22ème décimale qu'on peut avoir des différences.
Quand on a trouvé le produit des 10 premiers termes, pour trouver la solution avec l'infinité de termes, on va donc multiplier par un nombre proche de
Re: limite d'un produit (10^n-1)/10^n
MERCI !
J'ai compris la démo.
Et je retiens précieusement le bornage de ln(1+h).
Pourrais-tu valider ce que j'ai trouvé pour le produit (9/10) x (19/20) x (29/30) x... (10n-1)/10n ???
(J'ai trouvé que celui-ci tend vers zéro)
La méthode que tu m'as décrite ne fonctionne pas, car la suite descend tellement lentement que le produit est encore égal à 0,185... après 10 millions de termes.
J'ai compris la démo.
Et je retiens précieusement le bornage de ln(1+h).
Pourrais-tu valider ce que j'ai trouvé pour le produit (9/10) x (19/20) x (29/30) x... (10n-1)/10n ???
(J'ai trouvé que celui-ci tend vers zéro)
La méthode que tu m'as décrite ne fonctionne pas, car la suite descend tellement lentement que le produit est encore égal à 0,185... après 10 millions de termes.
Re: limite d'un produit (10^n-1)/10^n
Pour cette autre suite ) , avec les logarithmes à nouveau, on démontre que la limite est 0.
, avec les logarithmes à nouveau, on démontre que la limite est 0.
En fait, ta suite est 'similaire' à la somme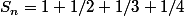 etc etc :
etc etc : ) est équivalent à
est équivalent à 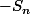
Cette somme tend vers +infini, mais très lentement.
tend vers +infini, mais très lentement.
Et donc tend vers 0.
tend vers 0.
En fait, ta suite est 'similaire' à la somme
Cette somme
Et donc
Re: limite d'un produit (10^n-1)/10^n
Bien !
Je suis content d'avoir trouvé une démo de même nature que la résolution de la nature illimitée de la série harmonique (par Euler je crois). J'ai construit une bijection entre Sn et une partie de Sn, qui m'amène à montrer que Sn<Sn. Quelle que soit la limite positive de Sn, Sn est plus petit...
Je suis content d'avoir trouvé une démo de même nature que la résolution de la nature illimitée de la série harmonique (par Euler je crois). J'ai construit une bijection entre Sn et une partie de Sn, qui m'amène à montrer que Sn<Sn. Quelle que soit la limite positive de Sn, Sn est plus petit...
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 2 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
