mathelot a écrit:est ce que l'équation pourrait ressembler à ça ? :
+\omega^2 (x-x_s)=0)
on réécrit l'équation:
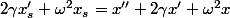 (1)
(1)où x' désigne la dérivée de x.
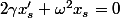 (2)
(2)(1): il s'agit d'une équation d'inconnue
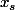
, linéaire,du premier ordre avec second membre.
Ses solutions sont celles de l'équation homogène (2) additionnées d'une solution particulière de l'équation (1).
résolution de l'équation (2):
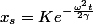
où K est une constante réelle.
Pour trouver une solution particulière de (1), on fait varier la constante K, on trouve:
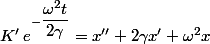
soit
 \, e^{\dfrac{\omega^2t}{2\gamma}}) (3)
(3)après , il faut trouver une primitive de K'...,i.e, intégrer le second membre de (3):
les solutions de (1) sont donc:
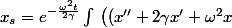 \, e^{\dfrac{\omega^2t}{2\gamma}} \right) dt +C e^{-\frac{\omega^2 t}{2 \gamma}})