DM de Maths, fonctions dérivée
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
hdci
- Membre Irrationnel
- Messages: 1962
- Enregistré le: 23 Juin 2018, 16:13
-
 par hdci » 28 Déc 2020, 20:31
par hdci » 28 Déc 2020, 20:31

Par "les mettre ensemble" je voulais simplement dire que -8 est une constate,
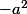
et une constante donc on les regroupe pour ne former "qu'un seul bloc de constante".
Ce n'est pas nécessaire mais cela permet d'avoir la forme
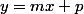
avec
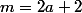
et

Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
-
Aurélien1608
- Membre Naturel
- Messages: 13
- Enregistré le: 15 Déc 2020, 19:15
-
 par Aurélien1608 » 29 Déc 2020, 00:10
par Aurélien1608 » 29 Déc 2020, 00:10
hdci a écrit:Yapuka mettre le
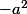
avec le
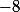
...
Aurélien1608 a écrit:oui donc j'obtiens y = a² + x (2a + 2) - 8
Attention, le signe devant

a disparu...
Oui il s'agissait juste d'une erreur d'inatention mais comment mettre ensemble -a² et -8 ensemble?
-
Aurélien1608
- Membre Naturel
- Messages: 13
- Enregistré le: 15 Déc 2020, 19:15
-
 par Aurélien1608 » 29 Déc 2020, 01:10
par Aurélien1608 » 29 Déc 2020, 01:10
hdci a écrit:
Par "les mettre ensemble" je voulais simplement dire que -8 est une constate,
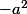
et une constante donc on les regroupe pour ne former "qu'un seul bloc de constante".
Ce n'est pas nécessaire mais cela permet d'avoir la forme
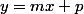
avec
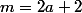
et

Ah oui d'accord, merci pour votre aide et par rapport à la deuxième partie de l'exercice, faut-il que je résolve l'equation du second degrès qui est notre expression du début pour trouver la réponse?
-
hdci
- Membre Irrationnel
- Messages: 1962
- Enregistré le: 23 Juin 2018, 16:13
-
 par hdci » 29 Déc 2020, 16:15
par hdci » 29 Déc 2020, 16:15
La seconde question ? Celle qui demande s'il y a des points de la courbe en-dessous de la tangente ?
Géométriquement, si je prends A et B alignés verticalement dans le repère, que signifie le fait que B se trouve en-dessous de A ?
Après avoir répondu à cette question préliminaire, on peut alors tenter de résoudre la question posée : on veut que la tangente soit en-dessous de la courbe.
Donc pour tout x, on veut que le point d'abcisse x de la tangente soit en-dessous du point d'abscisse x de la courbe.
En utilisant le résultat de la question préliminaire posée ci-dessus concernant les points A et B, on aboutit à une inéquation, qu'il n'y a plus qu'à résoudre... Dans le sens "on veut identifier a pour que ce soit vrai pour tous les x".
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 149 invités
avec le
...
Aurélien1608 a écrit:oui donc j'obtiens y = a² + x (2a + 2) - 8a disparu...
et une constante donc on les regroupe pour ne former "qu'un seul bloc de constante".
avec
et