Recurrence terminale
13 messages
- Page 1 sur 1
Re: Recurrence terminale
bonsoir
charge ton énoncé sur casimages.com et crée un lien sur le forum en direction de l'énoncé,
ou alors copie l'énoncé à la main.
charge ton énoncé sur casimages.com et crée un lien sur le forum en direction de l'énoncé,
ou alors copie l'énoncé à la main.
Re: Recurrence terminale
Soient a et b deux nombres réels. Une suite est dite arithmetico géométrique si elle vérifie la relation Un+1= a Un +b pour tout entier naturel b. Démontrer par récurrence que le terme général de la suite U est donné pour tout entier naturel par :
Un= a^n (Uo - b/(1-a) ) + b/(1-a)
Alors d'habitude j'arrive bien en recurrence mais là c'est un peu extrême comme niveau pour moi.
Je n'arrive même pas à faire l'initiation...
Voilà merci d'avance pour vous retour
Un= a^n (Uo - b/(1-a) ) + b/(1-a)
Alors d'habitude j'arrive bien en recurrence mais là c'est un peu extrême comme niveau pour moi.
Je n'arrive même pas à faire l'initiation...
Voilà merci d'avance pour vous retour

Re: Recurrence terminale
Uo=1*(Uo- b/(1-a)) +b/(1-a) = Uo
Effectivement je n'avais pas simplifié a^o merci.
Effectivement je n'avais pas simplifié a^o merci.
Re: Recurrence terminale
Pour l'hérédité: supposons que la propriété à prouver est vrai au rang n. Montrer que la propriété est vrai au rang n+1.
Un+1 = a*a^n ( Uo-b/(1-a))+b/(1-a)
J'ai donc a*Un mais pas +b
Un+1 = a*a^n ( Uo-b/(1-a))+b/(1-a)
J'ai donc a*Un mais pas +b
Re: Recurrence terminale
Considère l'égalité
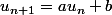 . remplace u_n par l'expression récurrente (au rang n)
. remplace u_n par l'expression récurrente (au rang n)
tu dois avoir un terme qui se calcule.
qui se calcule.
PS: avec
tu dois avoir un terme
PS: avec
Re: Recurrence terminale
Orelie22 a écrit:Pour l'hérédité: supposons que la propriété à prouver est vrai au rang n. Montrer que la propriété est vrai au rang n+1.
Un+1 = a*a^n ( Uo-b/(1-a))+ab/(1-a)+b
J'ai donc a*Un mais pas +b
Re: Recurrence terminale
mathelot a écrit:Considère l'égalité. remplace u_n par l'expression récurrente (au rang n)
tu dois avoir un termequi se calcule.
PS: avec
C'est à dire un terme ab/(1-a) ??
En tout cas, absolument rien dans l'énoncé
Re: Recurrence terminale
mathelot a écrit:Orelie22 a écrit:Pour l'hérédité: supposons que la propriété à prouver est vrai au rang n. Montrer que la propriété est vrai au rang n+1.
Un+1 = a*a^n ( Uo-b/(1-a))+ab/(1-a)+b
J'ai donc a*Un mais pas +b
Je t'ai indiqué en rouge ce qui n'allait pas dans ton calcul.
Puis réduis la somme ab/(1-a)+b
Re: Recurrence terminale
Oui j'ai bien pris note de ces modifications mais j'arrive tous de même à : Un+1 = a*a^n ( Uo-b/(1-a))+ab/(1-a)+b. Et non ua*a^n ( Uo-b/(1-a))+b/(1-a)+b
Il y a peu être une simplification qui m'a echappée...
Il y a peu être une simplification qui m'a echappée...
Re: Recurrence terminale
Orelie22 a écrit:Oui j'ai bien pris note de ces modifications mais j'arrive tous de même à : Un+1 = a*a^n ( Uo-b/(1-a))+ab/(1-a)+b. Et non a*a^n ( Uo-b/(1-a))+b/(1-a)+b
Il y a peu être une simplification qui m'a echappée...
i) il faut réduire a.a^n par un calcul sur les exposants
ii) il faut additionner ab/(1-a)+b en réduisant au même dénominateur 1-a
NB: la formule de récurrence au rang n+1 s'écrit
Re: Recurrence terminale
Effectivement cela se simplifié en (ab+b-ab)/(1-a) donc b/(1-a) merci beaucoup pour votre aide.
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 112 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
