Question vrai/faux

[Yokidok]

Bonsoir,
Voici le problème :

Soit H la fonction d´efinie sur R par la formule
H(x) =
ln(|x|) si x < 0,
sin x si x ≥ 0,
et u la fonction definie sur R par u(x) = −exp(x)
La fonction H ◦ u est-elle continue sur R.

J'ai fait les limite de chaque côté de la fonction H en 0 et elles sont différente la réponse serait donc non mais certains me disent que c'est vrai car -exp(x) prend que des valeurs dans R- et donc on a juste ln(exp(x)) =x
Je ne comprend pas

[phyelec]

Bonjour,

La fonction exponentielle est l'inverse de la fonction logarithme népérien, elle est définie, continue et croissante sur R :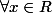 on a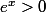

donc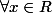 et ln(|)=ln()=x

[Yokidok]

La fonction H o u se résume donc à x ?
Donc continue sur R ?

[phyelec]

Bonjour,

pour x< 0, La fonction H(x)=x donc continue sur ]-, 0[
pour x >0 La fonction H(x)=sin(x) donc continue sur ]0,[

Que vaut-elle en 0?

[phyelec]

Bonjour,

je n'ai pas vu le >=0,pour x >=0 , La fonction H(x)=sin(x) donc continue sur [0, +\infty[
donc H est définie sur tout R donc continue sur R

[Yokidok]

Dans ce cas là,
H(X) =sin(x)?

[phyelec]

n'oubliez pas de faire la limite de H quand x tend vers

[Yokidok]

Oui mais H est une fonction composée
Donc cest différent non ?

[Yokidok]

Oui quand je passe aux limites
Je trouve des limites différents en 0+ et 0-

[phyelec]

Bonjour,

H(X) =sin(x) sur [0, +[ c'est l'énoncé.

en gros :
Il faut qu'en 0 les deux morceaux de H se "rejoignent" pour prouver la continuité.
pour x>= 0 la fonction H est définie en 0 et vaut 0. il faut vérifier que H(x) pour x<0 tend vers 0 quant x se rapproche de 0, mais en "venant des nombres négatifs"

[phyelec]

en bref que la limite en vaut 0

[phyelec]

En 0+ la fonction est définie c'est sin(0)=0

[Yokidok]

Ce n'est pas plutôt sin(-exp(0))?

[phyelec]

Bonjour ,
Voici votre énoncé :
oit H la fonction d´efinie sur R par la formule
H(x) =
ln(|x|) si x < 0,
sin x si x ≥ 0,
et u la fonction definie sur R par u(x) = −exp(x)

H est continue sur R, u= −exp(x) est continue sur H, Ho u est la composée de deux fonctions continues donc Ho u est continue.

[phyelec]

lire : u= −exp(x) est continue sur R

[phyelec]

H est continue sur R, u= −exp(x) est continue sur R, Ho u est la composée de deux fonctions continues sur R donc Ho u est continue R.

[Yokidok]

Je peux justifier avec votre réponse ?
La composée de deux fonctions continues est continue?

[phyelec]

Bonjour,

Il y a deux manières de faire :
1) démontrer que H et u sont continuent et dire que H o U est continue
ou
2) démontrer que Hou est continue.

Je pense que vous avez fait la deuxième.

[phyelec]

"La composée de deux fonctions continues est continue " , c'est doute dans votre cours.

si vous faites la méthode 1, vous avez juste à démontrer que H est continue.

[Yokidok]

En fait,
Je voulais montrer que H o u était continue avec un prolongement par contuité
J'ai donc fait :
La limite de H o u quand x tend vers 0- et même chose pour 0+
Mais certains de mes camarades me disent que -exp(x) prend uniquement des valeurs négatives
En gros, ils disent que jamais on aura le cas ou x <= 0 et donc sin(-exp(x))
Donc la fonction H o u se résume à : f(Hou) (x) = x
Qui est effectivement continue