Développement de Taylor

[mathlab1234]

Bonjour à tous,

J'ai un problème avec un devoir de modélisation statistique appliquée.


Y(m)=(exp(mX-m^2 /2)-1-mX)/d
d=(exp(m^2)-1-m^2)^1/2

J'ai besoin de savoir ce qui ce passe quand m=0 à l'aide d'un développement.
Voici le travail que j'ai effectué jusqu'à maintenant, mais je suis bloquée à la fin et très peu convaincue de mes calculs:
https://i.imgur.com/OmcAtbN.jpg

Je vous remercie d'avance pour toute aide.

[GaBuZoMeu]

J'ai joint le travail que j'ai effectué jusqu'à maintenant

Où ?

[mathlab1234]

J'ai joint le travail que j'ai effectué jusqu'à maintenant

Où ?

Bonjour, merci de votre remarque je ne m'étais pas rendue compte que la photo ne s'était pas uploadé . J'obtiens un message d'erreur quand j'essaye de la joindre à mon post, je l'ai donc complété d'un lien.

[GaBuZoMeu]

Qui est X ? Une quantité fixée ?
En tout cas, ton développement limité de d au voisinage de 0 est visiblement fait à un ordre insuffisant. Il faut pousser plus loin, à l'ordre 4.

[mathlab1234]

Qui est X ? Une quantité fixée ?
En tout cas, ton développement limité de d au voisinage de 0 est visiblement fait à un ordre insuffisant. Il faut pousser plus loin, à l'ordre 4.

On considère Xi fixé dans cette question .
J'y avais pensé, mais après je me retrouve avec la racine carrée d'un somme. Je ne sais pas comment simplifier cela.

[mathlab1234]

J'ai essayé de refaire mes calculs avec un DL de degré plus élevé au dénominateur.
https://imgur.com/UWw5BEW

Est ce cela vous semble juste?

[Black Jack]

Salut,

e^(mx-m²/2) = 1 + (mx-m²/2) + (mx-m²/2)²/2! + ...

e^(mx-m²/2) - 1 - mx = -m²/2 + (mx-m²/2)²/2! + ...
e^(mx-m²/2) - 1 - mx = -m²/2 + m²(x-(m/2))²/2 + ...

e^m² = 1 + m² + (m²)²/2 + ...
e^m² - 1 - m² = (m²)²/2 + ...
e^m² - 1 - m² = m^4/2 + ...
(e^m² - 1 - m²)^(1/2)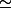 m²/V2

(e^(mx-m²/2) - 1 - mx)/V(e^m² - 1 - m²)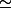 [-m²/2 + m²(x-(m/2))²/2 ]/[ m²/V2]

(e^(mx-m²/2) - 1 - mx)/V(e^m² - 1 - m²)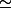 V2*[-1/2 + (x-(m/2))²/2 ]

lim(x-->0) [(e^(mx-m²/2) - 1 - mx)/V(e^m² - 1 - m²)] = V2.(-1/2 + x²/2)

lim(x-->0) [(e^(mx-m²/2) - 1 - mx)/V(e^m² - 1 - m²)] = (x²-1)/V2

Vérifie.