Développement de Taylor ??

[raito123]

Bonsoir,

J'ai un énoncé qui me pose un petit probléme :

Soit la fonction . Va falloir montrer que f est indéfiniment dérivable ( on montrera qe la dérivé d'ordre de f est de la forme ou P_n est un polynome !!

Le point qui me pose probléme c'est le "0" : doit-on admettre que f est continue en 0 ?? C'est vrai, elle admet une limite en 0 : doit-on alors prolonger la fonction par continuité en 0 ??

Aprés on me demande le développement de Taylor en 0 de f ? je présume qu'on considére que pour tout n la dérivé n-iéme de f est continue en 0, non?

Merci d'avance pour vos réponses !!

[Purrace]

Récurrence !Émet une conjecture en examinant les petits indices .

[raito123]

hein ??

merci pour ta réponse, mais en fait j'ai pas compris ce que tu veux dire ??

Sinon j'ai démontrer la relation pour x =! 0 mais pour x=0 je sais pas trop ce que je dois faire ? et en ce qui concerne le developpement : la fonction doit être continue non ?

[leon1789]

salut,
en zéro, il faut faire pour chaque un taux d'accroissement , et montrer que ce taux tend vers 0.
A+

[raito123]

faut déja avoir donc la continuité en 0, non ??

[Purrace]

Le fait qu'elle soit indefiniment derivable peut etre contenue dans l'hypothese de recurrence , tu peut prendre par exemple comme hypothese P(n): f est D^n sur R et il existe Pn tels que fderivé n-ieme=f(x)Pn(x)/x^3n!!

[raito123]

Ok !!

Et pour le développement de taylor on a :

mais les sont considérer nul, non ?

[Purrace]

1er point tu n'a pas justifier qu'elle était dérivable en 0 , secondo tu veut en faire quoi?

Et en plus si tu choisit juste par exemple f(0)=0 alors tu ne considéré plus f mais sa prolongé par continuité !

[raito123]

Le probléme c'est que j'arrive pas à comprendre le but de l'exo : on a même pas l'image de 0 par f alors pourquoi ils nous demandent de démontrer que f est D^n en plus de trouver le DLn(0) !??

[Purrace]

On demande pas le Dln en 0 mais de montrer par (recurrence) que fderivé nieme s'ecrit sous la forme demandé apres en en deduit une relation de recurrence sur le polynome Pn.

[raito123]

(...)

Et en plus si tu choisit juste par exemple f(0)=0 alors tu ne considéré plus f mais sa prolongé par continuité !

Doit-je comprendre qu'on doit considérer la prolongé par continuité de f en 0??

On demande pas le Dln en 0 mais de montrer par (recurrence) que fderivé nieme s'ecrit sous la forme demandé apres en en deduit une relation de recurrence sur le polynome Pn.

J'ai démontrer cela mais c'est la 2éme question qui me pose un probléme : quel est le dévellopement de Taylor en 0 ??

[Purrace]

Oui tu peut étendre l'ensemble de def de ta fonction si possible en posant f(0)=0 et essaye de regarder sur les crans supérieur !

[raito123]

et donc le DLn(0) serai : f(x)= o(x^n) puisque l'image de 0 ar la dérivé k-iéme est 0 ??

[Purrace]

Es tu sur ? Que fait Pn(x)/x^3n en 0 est ce que t'es sur que tu peux poser Pn(x)/x^3nf(x) egale à 0 en 0!

[raito123]

Ben oui la limite de Pn(x)/x^3nf(x) en 0 tend vers 0 (en plus on a supposer que f(0)=0), Je me trompe ??

[Purrace]

On a jamais montrer que Pn(x)/x^3nf(x)etait continue en 0 et en plus que ce valait 0????

[Purrace]

Je pense qu'il faudrait que tu regarde le degré de Pn

[raito123]

J'ai déja vu : j'ai trouver dP_n = 2(n-1) !! J'ai aussi trouver que P_n(0)=2^n !!

[raito123]

J'ai déja vu : j'ai trouver dP_n = 2(n-1) !! J'ai aussi trouver que P_n(0)=2^n !!

Ceci me donne pas grande chose puisque f^k(0) va quand même tendre vers 0 non ?

[leon1789]

Pardon, je n'ai pas lu les messages précédents, je suis un peu pressé là.

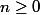
Il faut faire une récurrence pour dont l'hypothèse est
Hyp_n : >