Développement de Taylor

[nico2b]

Bonsoir, voici la question qui me pose problème...

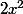
Soit f une fonction de . On suppose que le polynome p(x) = -1 + 4x - est le développement de Taylor de f en 1 d'ordre 2.

Dites si la fonction f atteint en 1 un minimum local, un maximum local, ou ni l'un ni l'autre. Justifiez votre réponse.


Mon idée était de retrouver la dérivé de la fonction pour pouvoir faire un tableau de signe...

Si je ne me trompe pas la dérivée vaut mais je ne sait pas si je suis sur la bonne voie...

Merci d'avance

[fahr451]

bonjour

j'ai toujours cru que la dérivée en un point était un nombre (appelé aussi nombre dérivé) ...

[nico2b]

Surement c'est pour ça que je demande de l'aide...

j'avais mit ceci car comme le développement de Taylor vaut

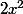
et p(x) = -1 + 4x - donc pour

i = 0 , on a -1

i = 1, on a 4x

i = 2, on a -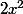

donc on aurait 4x = d'où ma réponse... Mais je me plante surement alors... Pourriez-vous m'expliquer?

Merci pour l'aide

[abel]

Tu devrais plutôt voir si p admet un max ou un min en 1 étant donné que f à le même "comportement" localement.

[nico2b]

Ok merci pour l'explication j'ai compris.
Je vais faire les calculs et je proposerai ma réponse....

Merci pour tout

[nico2b]

Juste un petit rappel pour le polynome il faut aussi dérivé une foix ou alors on recherche tt de suite les racines?

merci de votre aide

[abel]

Il faut faire une étude de fonction classique au voisinage de 1 de ta fonction polynomiale donc oui en passant par la dérivée pr rendre le truc plus pratique...apres, un tableau de variation de p suffira à voir si f admet un max ou un min en 1 étant donné que p et f ont le meme comportement local (au voisinage de 1).

[nico2b]

merci :we:

[nico2b]

J'ai comme réponse un maximum local ais-je bon?

[mathelot]

localement,


f admet donc un maximum local égal à en

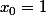
[nico2b]

merci :we: