Suite numérique

[thomas9841345]

Bonjour,

Voici un exercice :

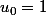
Soit la suite u définie sur par et .

1. Calculer les premiers termes de la suite u (on écrira ces termes sous forme de fractions irréductibles). Conjecturer alors une expression explicite de .
2. Démontrer la conjecture émise en question 1.


Ce que j'ai fait :
1.







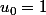
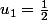
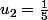
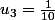
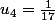
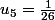
Conjecture :

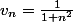
2. Démonstration :
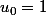
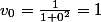
D'une part : et donc
D'autre part : je dois démontrer que = .

Mais c'est pour démontrer cette égalité que je bloque.
Merci de votre aide

[Sa Majesté]

Salut,

Une démonstration par récurrence fonctionne bien.
Tu as déjà fait l'initialisation, reste l'hérédité.

[thomas9841345]

Salut,

Une démonstration par récurrence fonctionne bien.
Tu as déjà fait l'initialisation, reste l'hérédité.

Je suis en première et il ne me semble pas que l'on ait abordé ce terme en cours. Une autre méthode serait-elle possible ?

[Sa Majesté]

2. Démonstration :
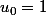
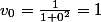
D'une part : et donc
D'autre part : je dois démontrer que = .

Tu n'as jamais vu les démonstrations par récurrence pourtant ce que tu as commencé à faire y ressemble.

Tu as montré que .

Tu supposes que pour un certain rank k, et tu montres que



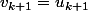
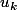
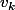
Tu remplaces par et tu simplifies.

[thomas9841345]

J'ai pu finir merci