Optimisation partie sous-différentiel
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ZLM
- Membre Naturel
- Messages: 56
- Enregistré le: 02 Juil 2018, 08:46
-
 par ZLM » 07 Oct 2019, 00:33
par ZLM » 07 Oct 2019, 00:33
Bonjour, s'il vous plaît, aider moi a résoudre cet exercice.
Exercice
Soit

un espace normé et
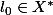
privé de 0.
On pose
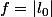
Montrer que
=\left( -1, 1\right) l_0)
.
)
est l'intervalle ouvert en -1 et 1.
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 07 Oct 2019, 06:19
par Sylviel » 07 Oct 2019, 06:19
Bonjour,
je ne comprends pas la définition de f. Telle qu'elle est écrite il s'agit d'une fonction constante...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6145
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 07 Oct 2019, 06:42
par GaBuZoMeu » 07 Oct 2019, 06:42
C'est un exercice d'application de la définition de sous-différentiel.
Peux-tu nous rappeler cette définition ?
@Sylviel : la valeur absolue d'une forme linéaire n'est pas une constante.
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 07 Oct 2019, 09:01
par Sylviel » 07 Oct 2019, 09:01
Ok, j'avais mal interprété.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
ZLM
- Membre Naturel
- Messages: 56
- Enregistré le: 02 Juil 2018, 08:46
-
 par ZLM » 11 Oct 2019, 22:01
par ZLM » 11 Oct 2019, 22:01
Bonjour à tous, merci déjà pour les différentes aides.
La définition est la suivante :
On dit que

est une minorante de

si
\leq f(x))
, pour tout
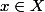
, et une minorante excate en
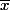
si
=f(\bar{x}))
.
On appelle sous-différentiel de

en
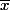
, l'ensemble des minorantes affines excates de

au point
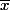
.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6145
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 12 Oct 2019, 09:12
par GaBuZoMeu » 12 Oct 2019, 09:12
Bon, il ne te reste plus qu'à appliquer cette définition pour vérifier que le sous-différentiel de

en 0 est bien ce qui est écrit.
Tu peux commencer par le plus simple ; montrer que les

avec

réel tel que

sont bien des minorantes affines exactes en 0 de

.
-
ZLM
- Membre Naturel
- Messages: 56
- Enregistré le: 02 Juil 2018, 08:46
-
 par ZLM » 13 Oct 2019, 22:53
par ZLM » 13 Oct 2019, 22:53
Merci beaucoup pour les indications. J'ai pu résoudre la question grâce à vos indications.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6145
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 14 Oct 2019, 05:50
par GaBuZoMeu » 14 Oct 2019, 05:50
Avec plaisir.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités