R^2 ouvert ?
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Ririyeman
- Membre Naturel
- Messages: 53
- Enregistré le: 04 Déc 2018, 23:54
-
 par Ririyeman » 01 Oct 2019, 18:35
par Ririyeman » 01 Oct 2019, 18:35
Bonjour je cherche a démontrer que R^2 est ouvert mais je bloque

/
Je sais qu'un espace est ouvert si pour tout x il existe un r tel que la boule de centre x et de rayon r est inclus dans l ensemble .
Donc pour R^2 ça parait evident que c'est un ouvert puisqu'on peut y caler autant de boule qu'on veut on pourra toujours trouver un rayon tq il soit inclus comme c'est un espace infini mais je n'arrive pas a le démontrer rigoureusement ...
Pourriez vous me donnez des pistes svp ? merci bonne soirée
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 01 Oct 2019, 19:27
par pascal16 » 01 Oct 2019, 19:27
pour toute norme utilisée
pour tout élément que l'on choisi de R²
la boule ouverte B de rayon 1 et de centre l'élément choisi est incluse dans R².
ai-je fait une erreur ?
-
LB2
- Habitué(e)
- Messages: 1504
- Enregistré le: 05 Nov 2017, 16:32
-
 par LB2 » 01 Oct 2019, 19:50
par LB2 » 01 Oct 2019, 19:50
@pascal16 : non c'est bon.
@Ririyeman : ta définition d'un ouvert est fausse. un ensemble est ouvert si pour tout x il existe un r tel que la boule ouverte de centre x et de rayon r est inclus dans l ensemble
Il faut ensuite la vérifier avec précision et rigueur notamment dans l'utilisation des quantificateurs. Sinon ce n'est pas des maths mais du gloubi boulga
-
Ririyeman
- Membre Naturel
- Messages: 53
- Enregistré le: 04 Déc 2018, 23:54
-
 par Ririyeman » 01 Oct 2019, 21:14
par Ririyeman » 01 Oct 2019, 21:14
LB2 a écrit:@pascal16 : non c'est bon.
@Ririyeman : ta définition d'un ouvert est fausse. un ensemble est ouvert si pour tout x il existe un r tel que la boule ouverte de centre x et de rayon r est inclus dans l ensemble
Il faut ensuite la vérifier avec précision et rigueur notamment dans l'utilisation des quantificateurs. Sinon ce n'est pas des maths mais du gloubi boulga
Exact autant pour moi :p et c'est cette rigueur que je recherche parce que ma seul piste c'est que R^2 est infini et contient toute les boules ouvertes de rayon r
pascal16 a écrit:pour toute norme utilisée
pour tout élément que l'on choisi de R²
la boule ouverte B de rayon 1 et de centre l'élément choisi est incluse dans R².
ai-je fait une erreur ?
Je pensais a ça également mais ça ma parait pas assez calculatoire

/
-
Tuvasbien
- Membre Relatif
- Messages: 440
- Enregistré le: 28 Fév 2019, 00:59
-
 par Tuvasbien » 01 Oct 2019, 21:24
par Tuvasbien » 01 Oct 2019, 21:24
Comme tu le dis si bien, c'est évident ! Si
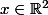
, alors toute boule centrée en

est incluse dans

. En effet,
=\{y\in\mathbb{R}^2,\ \|x-y\|<r\}\subset\mathbb{R}^2)
.
-
Ririyeman
- Membre Naturel
- Messages: 53
- Enregistré le: 04 Déc 2018, 23:54
-
 par Ririyeman » 01 Oct 2019, 21:39
par Ririyeman » 01 Oct 2019, 21:39
Tuvasbien a écrit:Comme tu le dis si bien, c'est évident ! Si
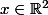
, alors toute boule centrée en

est incluse dans

. En effet,
=\{y\in\mathbb{R}^2,\ \|x-y\|<r\}\subset\mathbb{R}^2)
.
Bon bah j'ai bloqué pour rien autant pour moi merci :')
-
GaBuZoMeu
- Habitué(e)
- Messages: 6133
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 01 Oct 2019, 22:02
par GaBuZoMeu » 01 Oct 2019, 22:02
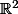
est ouvert
dans  ,
, c'est assez tautologique !
-
Fradel22
- Messages: 2
- Enregistré le: 02 Oct 2019, 08:50
-
 par Fradel22 » 02 Oct 2019, 12:33
par Fradel22 » 02 Oct 2019, 12:33
Bonjour,
Je crois que GaBuZoMeu pointe du doigt la vraie question :
IR² ouvert dans quoi ?
Par exemple, si on me demande " [2, 7[ est-il ouvert ? " Je serai bien en peine de répondre à cette question.
Si la question est "[2, 7[ est-il un ouvert de IR ? " La réponse est non, mais il est clair que [2, 7[ est un ouvert de [2,7[ (et aussi un fermé)
------
NB : désolé de ne pas utiliser l'éditeur d'équation, mais lorsque je clique sur "copy to document", cela ferme la réponse que je suis en train d'écrire (sans récupération possible)
-
LB2
- Habitué(e)
- Messages: 1504
- Enregistré le: 05 Nov 2017, 16:32
-
 par LB2 » 02 Oct 2019, 14:27
par LB2 » 02 Oct 2019, 14:27
Tout à fait d'accord avec Fradel22 et GBZM (mais c'est déjà un deuxième niveau d'abstraction par rapport à la question de base)
-
Ririyeman
- Membre Naturel
- Messages: 53
- Enregistré le: 04 Déc 2018, 23:54
-
 par Ririyeman » 02 Oct 2019, 20:57
par Ririyeman » 02 Oct 2019, 20:57
Fradel22 a écrit:Bonjour,
Je crois que GaBuZoMeu pointe du doigt la vraie question :
IR² ouvert dans quoi ?
Par exemple, si on me demande " [2, 7[ est-il ouvert ? " Je serai bien en peine de répondre à cette question.
Si la question est "[2, 7[ est-il un ouvert de IR ? " La réponse est non, mais il est clair que [2, 7[ est un ouvert de [2,7[ (et aussi un fermé)
------
NB : désolé de ne pas utiliser l'éditeur d'équation, mais lorsque je clique sur "copy to document", cela ferme la réponse que je suis en train d'écrire (sans récupération possible)
Ouai comme le dis GaBuZoMeu c'est tellement tautologique que j'avais pas compris et je parlais bien de R^2 dans R^2 qui est ouvert ( mais aussi fermé )
-
sofianmakhlouf
- Membre Naturel
- Messages: 72
- Enregistré le: 03 Oct 2019, 15:54
-
 par sofianmakhlouf » 05 Oct 2019, 22:50
par sofianmakhlouf » 05 Oct 2019, 22:50
Tuvasbien a écrit:Comme tu le dis si bien, c'est évident ! Si
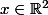
, alors toute boule centrée en

est incluse dans

. En effet,
=\{y\in\mathbb{R}^2,\ \|x-y\|<r\}\subset\mathbb{R}^2)
.
Peut on prendre r=1 ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
 /
/