Nombre complexe
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
xD55
- Membre Naturel
- Messages: 29
- Enregistré le: 11 Sep 2019, 10:16
-
 par xD55 » 17 Sep 2019, 21:47
par xD55 » 17 Sep 2019, 21:47
Bonjour, pouvez-vous m'aider à résoudre cette question suivant :
on considéré , dans C l équation (E) : z^3-2(√3+i)z^2+4(1+i√3)z-8i=0
montrer que (E) admet une solution imaginaire pure que l'on déterminera.
merci bcp d avance de m aider


-
Tuvasbien
- Membre Relatif
- Messages: 440
- Enregistré le: 28 Fév 2019, 00:59
-
 par Tuvasbien » 18 Sep 2019, 00:12
par Tuvasbien » 18 Sep 2019, 00:12
Un imaginaire pur s'écrit sous la forme
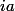
avec
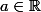
, or
^3-2(\sqrt{3}+i)(ia)^2+4(1+i\sqrt{3})(ia)-8i=-ia^3+2a^2(\sqrt{3}+i)+4ia(1+i\sqrt{3})-8i)
On cherche

tel que cette expression s'annule, en regroupant parties réelle et imaginaire on a

et

ou encore en simplifiant :

et

Il n'y a qu'un seul

qui convient, à toi de trouver lequel.
-
xD55
- Membre Naturel
- Messages: 29
- Enregistré le: 11 Sep 2019, 10:16
-
 par xD55 » 20 Sep 2019, 18:26
par xD55 » 20 Sep 2019, 18:26
Merci bcp
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 95 invités