Equation à 2 inconnues

[florian699]

Bonjour,

j'écris sur ce forum car j'ai un problème d'équation que je n'arrive pas à résoudre.
Je suis dans le domaine de la biologie est j'essaie d'équilibrer une formule pour des plantes (engrais).

La problématique est la suivante :
Je dois trouver 2 valeurs à partir de 2 autres valeurs.

J'ai en tout 4 valeurs : 2 que je connais (C1 et C2) et 2 que je dois trouver (M1 et M2).

C1 et C2 sont tous les 2 compris entre 1.00 et 2.00 (ex : M1=1.3 et M2=1.9)
M1 et M2 sont tous les 2 compris entre 1.00 et 100.00 (mais je ne connais pas les valeurs de M1 et M2).

Je recherche les valeurs de M1 et M2 en sachant les 2 règles ci-dessous doivent être respectées :
C1 x M1 doit être >= M1 + M2
C2 x M2 doit être >= M1 + M2

J'espère avoir été clair.

Je pense qu'une équation pourrait régler cela.
Merci à l'avance pour votre aide car moi et les équations cela fait pas bon ménage.

[GaBuZoMeu]

Avec les conditions que tu imposes, on a 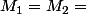n'importe quoi entre 1 et 100 ( et forcément )
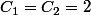Ça te semble raisonnable ?

[florian699]

Merci pour ta réponse.
M1 ne peut être égale à M2 car C1 et C2 sont obligatoirement différents (c'est vrai que je l'ai pas précisé).

J'ai écrit une bétise dans mon exemple ci dessus : (ex : M1=1.3 et M2=1.9) en fait il fallait comprendre (ex : C1=1.3 et C2=1.9) et non M1 et M2.

[GaBuZoMeu]

J'avais compris que tu avais fait une coquille.

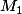est obligatoirement égal à 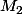avec les conditions que tu poses :
puisque et , on a , d'où .
puisque et , on a , d'où .
Donc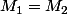 , et ça entraîne .

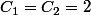Revois ton problème. Tu t'es visiblement trompé en le modélisant.