Congruence

[Emojigrin]

Résoudre l'équation suivante :

119x≡17 [51]

On donnera la réponse sous une forme générale dépendant d'un entier relatif quelconque
k
k, par exemple :
{3k+2 ; 6k+1,k∈Z}.

[Emojigrin]

Bonjour je bloque sur cet exo pourriez vous m'aider ?
Merci d'avance

[capitaine nuggets]

Salut !

En faisant la division euclidienne de par 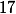, on a (mod 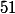). Sachant que , tu n'as plus qu'en déduire qu'il existe un entier tel que

[Lostounet]

Résoudre l'équation suivante :

119x≡17 [51]

On donnera la réponse sous une forme générale dépendant d'un entier relatif quelconque
k
k, par exemple :
{3k+2 ; 6k+1,k∈Z}.

Il y a plusieurs méthodes possibles.

Une méthode possible (mais qui ne marche pas ici malheureusement) est de chercher un entier n tel que 119n = 1 [mod 51]

Si on trouve un tel entier n, il suffira de multiplier les deux côtés de 119x = 17 [mod 51] par n. Cela donnerait:

(119n)x=17n [mod 51]
Donc x=17n (mod 51)

Par contre cela ne marche pas ici car il n'existe pas un tel entier n ! Dans d'autres exos ça peut marcher.

Il y a plusieurs manières de contourner le problème, comme la méthode de Capitaine Nuggets.


Tu peux aussi chercher à résoudre l'équation diophantienne: 119x - 51y = 17
Si tu as vu ça en cours.

[Emojigrin]

Alors pour la première methode ce qui me derange c’est le fait de diviser alors que les congruences ne sont pas compatibles avec la division.
Pour l’equation diophantienne je bloc pour trouver une solution evidente de 119x-51y=1
Merci de vos reponses

[Emojigrin]

Oubliez ce que j’ai dit pour la premiere methode

[Lostounet]

Alors pour la première methode ce qui me derange c’est le fait de diviser alors que les congruences ne sont pas compatibles avec la division.
Pour l’equation diophantienne je bloc pour trouver une solution evidente de 119x-51y=1
Merci de vos reponses

Oui ! Tu es tombé dans le piège !

119x - 51y = 17

Tu dois impérativement simplifier l'équation avant de poursuivre...
Aide:
7*17x - 3*17y = 17*1
On peut tout diviser par 17.

Si tu ne la simplifies pas... On ne pourra pas appliquer l'algorithme d'Euclide (7 et 3 sont premiers entre eux donc on va trouver 1 à la fin mais 119 et 51 ne sont pas premiers entre eux donc la méthode du cours ne s'applique pas directement).
Justement 119x-51y=1 n'a pas de solution car 119 et 51 ne sont pas premiers entre eux. Par contre 7x-3y=1 possède des solutions.