Salut
Dans un exo on a :
f un endomorphisme de R^3 tq
f^2-5f+6id=0
Je veux déterminer tous les f vérifiant cette condition.
Je l 'ai factorisé : (f-2id)(f-3id) =0 alors (f(x)-2x)(f(x)-3x)=0 ..est ce que je peux déduire que la solution c'est
f:R^3-->R^3
x------>2x
Ou
f:R^3-->R^3
x----->3x
Cordialement
Endomorphisme en équation
4 messages
- Page 1 sur 1
Re: Endomorphisme en équation
Salut, c'est l'endomorphisme qui à
c'est l'endomorphisme qui à \!\in\!\R^3) associe
associe \!\in\!\R^3) .
.
- Peut tu me dire ce que c'est que ?
?
- Et(f\!-\!3id)) , c'est quoi ?
, c'est quoi ?
- Et si on prend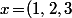\!\in\!\R^3) , c'est quoi
, c'est quoi \!-\!2x)(f(x)\!-\!3x)) ?
?
Bon, ben prenons l'exemple simple oùNAJMA a écrit:f^2-5f+6id=0 . . .
Je l 'ai factorisé : (f-2id)(f-3id) =0 alors (f(x)-2x)(f(x)-3x)=0
- Peut tu me dire ce que c'est que
- Et
- Et si on prend
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Endomorphisme en équation
f^2-5f+6id c'est un endomorphisme
Je ne sais pas ce que vous voulez me dire ?
Je ne sais pas ce que vous voulez me dire ?

Re: Endomorphisme en équation
Je pence que la solution c'est 2 fois la matrice identité ou 3 fois la matrice identité d'après ta factorisation donc ici f=2*(id) ou f=3*(id). Je pence que tu dois revoir la définition d'un endomorphisme.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
