Dénombrabilité

[schelde]

Bonjour,

Je cherche à justifier que, si est une suite d'un espace vectoriel quelconque, alors, l'ensemble
est denombrable.

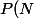En fait, ce qui me gêne surtout là dedans, c'est que, a priori, est un sous ensemble (fini) quelconque de . Or, n'est pas denombrable...

Quelqu'un aurait il une idée ?

Merci d'avance !

[arnaud32]

ici tu as qui est une union denombrable de parties finies, donc denombrable

[LB2]

L'ensemble des parties de , , n'est pas dénombrable.
En revanche, l'ensemble des parties finies de , , est dénombrable comme union dénombrable de dénombrables.

[Ben314]

Salut,
Et il y a même une bijection on ne peut plus simple et naturelle entre les parties finies de N et N lui même :
A une partie finie de N, tu associe l'entier qui, en base 2, s'écrit avec des 1 aux "positions" correspondant aux éléments de la partie en question : c'est on ne peut plus clairement bijectif.
Par exemple à la partie A={0,1,5,6,8} tu associe N=101100011 en base 2, c'est à dire
N = 2^0+2^1+2^5+2^6+2^8 = 355

[schelde]

Ok, merci beaucoup !