Dénombrabilité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par legeniedesalpages » 25 Sep 2007, 22:52
par legeniedesalpages » 25 Sep 2007, 22:52
Bonsoir,
je n'arrive pas à démarrer sur cet exercice:
1) Montrer que l'ensemble des applications de

dans
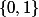
est équipotent à
)
, ensemble des parties de

.
2) Le produit cartésien d'une famille dénombrable d'ensemble au plus dénombrable est-il au plus dénombrable?
Merci pour vos indications

-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 25 Sep 2007, 22:56
par fahr451 » 25 Sep 2007, 22:56
bonsoir
N n 'y est pour rien
prends E un ensemble quelconque
phi : P(E) -> F (E,{0,1 })
A -> phi(A) où phi (A) est la fonction caractéristique de A (vaut 1 sur A et 0 sur le complémentaire)
phi est bijective
2) cf 1) ... avec N cette fois
 par legeniedesalpages » 25 Sep 2007, 22:58
par legeniedesalpages » 25 Sep 2007, 22:58
je pensais utiliser le fait que pour une suite

, il existe unique ensemble
)
défini par
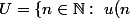=1\})
du coup j'ai une bijection non?
 par legeniedesalpages » 25 Sep 2007, 23:00
par legeniedesalpages » 25 Sep 2007, 23:00
bonsoir fahr,
désolé je n'avais pas vu ton post,
merci pour tes éclaircissements.
 par legeniedesalpages » 26 Sep 2007, 01:28
par legeniedesalpages » 26 Sep 2007, 01:28
pour montrer que

est non dénombrable, je ne vois pas comment procéder?
est-ce que je peux dire que
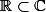
ou seulement qu'il existe une injection de

dans

?
 par legeniedesalpages » 26 Sep 2007, 02:51
par legeniedesalpages » 26 Sep 2007, 02:51
encore un autre exo où je bloque dès la première question:
Soit

un ensemble dénombrable.
1) Montrer que, pour tout entier
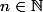
, l'ensemble des parties de

ayant au plus

éléments est dénombrable.
2) En déduire que l'ensemble des parties
finies de

est dénombrable.
3) L'ensemble de toutes les parties de

est-il dénombrable?
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 26 Sep 2007, 09:10
par fahr451 » 26 Sep 2007, 09:10
bonjour
on peut écrire
J = { x(k) k dans N }
posons
E (k) = { x(i) i=< k }, E(k) est fini
et P( E(k), n) ) l'ensemble des parties à au plus n éléments de E(k)
ensemble fini
on a l'ensemble des parties de J à au plus n éléments = U P(E(k) ,n) qui est donc dénombrable (l'union porte sur k et n'est pas disjointe)
 par legeniedesalpages » 26 Sep 2007, 10:44
par legeniedesalpages » 26 Sep 2007, 10:44
Bonjour fahr,
désolé je ne comprends pas.

est l'ensemble des termes d'une suite
)
, mais cette suite est à valeurs dans quoi? dans

?
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 26 Sep 2007, 10:51
par fahr451 » 26 Sep 2007, 10:51
ah oui j'ai fait une coquille
ce E là c 'est ton J bien sûr (quelle idée d'appeler J l ensemble :id: )
et le dernier J c'est l'ensemble des parties à au plus n éléments
je corrige
 par legeniedesalpages » 26 Sep 2007, 10:55
par legeniedesalpages » 26 Sep 2007, 10:55
ah ok, et donc

est une bijection de

dans

?
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 26 Sep 2007, 10:58
par fahr451 » 26 Sep 2007, 10:58
oui une numération de J
 par legeniedesalpages » 26 Sep 2007, 11:09
par legeniedesalpages » 26 Sep 2007, 11:09
ok, je crois que j'ai compris, donc il me reste à montrer que l'ensemble des parties de J à au plus n éléments est infini pour montrer qu'il est dénombrable.
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 26 Sep 2007, 11:12
par fahr451 » 26 Sep 2007, 11:12
est ce dur?
n>0
il ya déjà tous les singletons en nombre infini
 par legeniedesalpages » 26 Sep 2007, 11:14
par legeniedesalpages » 26 Sep 2007, 11:14
ah oui c'est vrai :briques:
merci pour ton aide fahr :)
-
SimonB
 par SimonB » 26 Sep 2007, 15:44
par SimonB » 26 Sep 2007, 15:44
Tes conventions ne disent-elles pas qu'un ensemble fini est dénombrable ?
(Les conventions à ce sujet semblent varier, selon l'humeur du rédacteur...)
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 26 Sep 2007, 15:45
par fahr451 » 26 Sep 2007, 15:45
à partir du moment où il emploie "au plus dénombrable" c'est que non
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités