Dénombrabilité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
arnaud26
- Membre Naturel
- Messages: 20
- Enregistré le: 20 Nov 2007, 03:08
-
 par arnaud26 » 26 Nov 2007, 22:29
par arnaud26 » 26 Nov 2007, 22:29
J'ai deux questions quant à la dénombrabilité, les voici
1) On sait que

est dénombrable et donc qu'on peut énumérer les nombres rationnels. Est-ce rigoureux d'écrire : soit

, la suite de tous les nombres rationnels ?
2) Si j'ai une suite d'ensemble
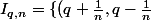 : q \in \mathbb{Q}, n\in \mathbb{N}\})
, est-ce correct de les définir comme
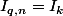
si non comment les définir avec un seul indice naturel ?
Merci de votre aide
 par legeniedesalpages » 26 Nov 2007, 22:31
par legeniedesalpages » 26 Nov 2007, 22:31
arnaud26 a écrit:J'ai deux questions quant à la dénombrabilité, les voici
1) On sait que

est dénombrable et donc qu'on peut énumérer les nombres rationnels. Est-ce rigoureux d'écrire : soit

, la suite de tous les nombres rationnels ?
2) Si j'ai une suite d'ensemble
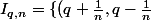 : q \in \mathbb{Q}, n\in \mathbb{N}\})
, est-ce correct de les définir comme
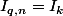
si non comment les définir avec un seul indice naturel ?
Merci de votre aide
Salut pour la 1), pour être encore plus rigoureux, il vaut mieux dire
soit

,
une suite de tous les nombres rationnels.
On peut énumérer de pleins de façons les nombres rationnels.
 par legeniedesalpages » 26 Nov 2007, 22:34
par legeniedesalpages » 26 Nov 2007, 22:34
Pour la 2), considèrer une bijection de

dans

(on sait qu'il en existe).
C'est ce qui est sous-entendu dans ta définition, et je pense qu'elle est correcte pour cause de flemme de rentrer dans des détails techniques en général.
-
arnaud26
- Membre Naturel
- Messages: 20
- Enregistré le: 20 Nov 2007, 03:08
-
 par arnaud26 » 26 Nov 2007, 22:34
par arnaud26 » 26 Nov 2007, 22:34
d'accord merci, ne me manque plus que le numéro 2 alors.
-
arnaud26
- Membre Naturel
- Messages: 20
- Enregistré le: 20 Nov 2007, 03:08
-
 par arnaud26 » 26 Nov 2007, 22:37
par arnaud26 » 26 Nov 2007, 22:37
ok merci beaucoup ca répond parfaitement à mes questions
-
Lierre Aeripz
- Membre Relatif
- Messages: 276
- Enregistré le: 14 Mai 2007, 17:31
-
 par Lierre Aeripz » 26 Nov 2007, 23:21
par Lierre Aeripz » 26 Nov 2007, 23:21
Attention cependant au piège classique : on peut prendre une suite parcourant tous les rationnels, mais on ne peut pas la prendre croissante. On ne peut pas dire "quitte à renuméroter, prenons une suite croissante", même si on se limite aux rationnels positifs.
 par legeniedesalpages » 26 Nov 2007, 23:25
par legeniedesalpages » 26 Nov 2007, 23:25
Bonjour Lierre Aeripz, je n'avais jamais pensé à ça.
Comment peut-on montrer qu'on ne peut attraper une telle suite? :hein:
-
arnaud26
- Membre Naturel
- Messages: 20
- Enregistré le: 20 Nov 2007, 03:08
-
 par arnaud26 » 27 Nov 2007, 01:10
par arnaud26 » 27 Nov 2007, 01:10
Une telle suite ne peut exister car on ne peut pas trouver deux rationnels consécutifs. Par la densité des rationnels dans les réels, entre supposons x_k et x_k+1, il va y avoir une infinité de rationnels.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 27 Nov 2007, 21:01
par leon1789 » 27 Nov 2007, 21:01
arnaud26 a écrit:Une telle suite ne peut exister car on ne peut pas trouver deux rationnels consécutifs. Par la densité des rationnels dans les réels, entre supposons x_k et x_k+1, il va y avoir une infinité de rationnels.
Je trouve que "densité de Q dans R" est un bien grand mot !
Disons simplement qu'entre deux rationnels x et y , il y a leur moyenne (x+y)/2. Cela suffit pour assurer l'impossibilité.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 15 invités
est dénombrable et donc qu'on peut énumérer les nombres rationnels. Est-ce rigoureux d'écrire : soit
, la suite de tous les nombres rationnels ?
, est-ce correct de les définir comme
si non comment les définir avec un seul indice naturel ?