Bonsoir j’ai besoin d’aide pour un DM en Math je suis bloqué :
Étudier les variations de la fonction f défini par f(x) : x^2*e^-x sur son ensemble de derivabilité.
J’ai définie sur R* =[0;+oo[ et j’ai voulu faire la limite de f(x)quand x—> 0 et j’ai trouvé 0
Donc limite de f(x) quand x tend vers 0=0 mais pour la limite de f(x) quand x tend vers +oo je trouve une forme indéterminée et si j’utili La bonne méthode je ne sais pas comment lever la forme indéterminée mais si j’en n’util Pas la bonne méthode pouvez-vous m’aide à trouvé s’il vous plaît merci
Math
5 messages
- Page 1 sur 1
Re: Math
f(x)=x^2*e^-x
si x= -1, est-ce que tu peux calculer sa valeur ?
Pourquoi ne peut-on pas utiliser R entier ?
pour la limite, qu'as-tu vu comme "croissance comparée" entre les puissance de x et la fonction exponentielle ?
si x= -1, est-ce que tu peux calculer sa valeur ?
Pourquoi ne peut-on pas utiliser R entier ?
pour la limite, qu'as-tu vu comme "croissance comparée" entre les puissance de x et la fonction exponentielle ?
Re: Math
Oui je peux trouver une valeur qui sera positive
Je ne peux pas utiliser R entier car la fonction est définie sur [0;+oo[
Non je n’ai pas cela
Je ne peux pas utiliser R entier car la fonction est définie sur [0;+oo[
Non je n’ai pas cela
Re: Math
la fonction 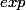 tend vers
tend vers  plus rapidement que toute
plus rapidement que toute
fonction polynomiale quand sa variable tend vers .
.
En particulier on a : ;
;
Pour ton exercice ; on a :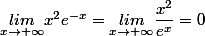 .
.
fonction polynomiale quand sa variable tend vers
En particulier on a :
Pour ton exercice ; on a :
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 97 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
