Bonsoir tout le monde,
Après avoir démontrer que SL2(Z) est un groupe.
SL2(Z) étant les matrices 2x2 dont leur déterminant=1.
Voici la question avec laquelle j'ai quelques soucis :
Prouver que si M (appartenant à SL2(Z)) a ordre fini m alors m appartient à {2,3,4,6}.
Mon problème c'est :
(M étant la matrice dont la première ligne = a b et la seconde = c d)
Si M a pour ordre m cela signifie que M à la puissance m est égal à la matrice identité. ( M étant l'élement du groupe SL2(Z)
Si m=2 :
Cela signifie que M²=Id
En calculant la matrice M², j'obtiens un système à 5 équations les 4 plus celle obtenue avec le déterminant de M qui doit être égale à 1 et il m'est impossible de trouver a b c d donc m ne peut être égale à 2 d'où mon problème avec l'énoncé.
C'est pourquoi j'aurai aimé savoir ce qui cloque avec ce que j'ai fait :).
Merci.
Dububu.
Groupes de matrices
10 messages
- Page 1 sur 1
j'ai peur de mal comprendre le sens de l'ordre d'un de M.
M appartient à SL2(Z)
Ce que je comprends par le sens de l'ordre de M c'est l'ordre de l'élément du groupe SL2(Z) et donc que M^m=Id .
(Cela ne signifie pas que M est une matrice mxm si m est l'ordre enfin ce que je crois)
Je ne sais pas à quoi me servirait Cayley-Hamilton.
M appartient à SL2(Z)
Ce que je comprends par le sens de l'ordre de M c'est l'ordre de l'élément du groupe SL2(Z) et donc que M^m=Id .
(Cela ne signifie pas que M est une matrice mxm si m est l'ordre enfin ce que je crois)
Je ne sais pas à quoi me servirait Cayley-Hamilton.
Bonsoir,
M est annulée par le polynôme qui est à racines simples dans
qui est à racines simples dans  , donc elle est diagonalisable dans
, donc elle est diagonalisable dans ) , et ses valeurs propres sont des racines de
, et ses valeurs propres sont des racines de  , donc des racines m-ièmes de l'unité, et comme M est d'ordre exactement m ces valeurs propres doivent être des racines primitives m-ièmes de l'unité. On peut calculer Tr M en fonction des valeurs propres, et
, donc des racines m-ièmes de l'unité, et comme M est d'ordre exactement m ces valeurs propres doivent être des racines primitives m-ièmes de l'unité. On peut calculer Tr M en fonction des valeurs propres, et  ...
...
Dububu : tu pars dans la mauvaise direction dans tes calculs, on demande de prouver que si m est d'ordre fini, alors cet ordre est 2, 3, 4 ou 6, on ne demande pas de montrer qu'il y a des matrices de ces ordres, toi tu essaies de trouver des matrices d'ordre 2, que tu trouves ou pas ça ne sert à rien pour l'exercice (mais on sait qu'il y en a : -Id est dans) et est d'ordre 2). Si on voulait résoudre de manière complètement calculatoire cet exercice il faudrait trouver les équations vérifiées par les entiers relatifs a, b, c et d tels que la matrice
et est d'ordre 2). Si on voulait résoudre de manière complètement calculatoire cet exercice il faudrait trouver les équations vérifiées par les entiers relatifs a, b, c et d tels que la matrice  soit de déterminant 1 et d'ordre m, et montrer que ces équations n'ont pas de solution si
soit de déterminant 1 et d'ordre m, et montrer que ces équations n'ont pas de solution si  , ce qui risque d'être assez fastidieux (il faudrait calculer les coefficients de la puissance m-ième de M en fonction des coefficients de M, pour tout m)...
, ce qui risque d'être assez fastidieux (il faudrait calculer les coefficients de la puissance m-ième de M en fonction des coefficients de M, pour tout m)...
M est annulée par le polynôme
Dububu : tu pars dans la mauvaise direction dans tes calculs, on demande de prouver que si m est d'ordre fini, alors cet ordre est 2, 3, 4 ou 6, on ne demande pas de montrer qu'il y a des matrices de ces ordres, toi tu essaies de trouver des matrices d'ordre 2, que tu trouves ou pas ça ne sert à rien pour l'exercice (mais on sait qu'il y en a : -Id est dans
Le théorème de cayley-Hamilton affirme que le polynôme X²-tX+1 annule la matrice M. L'entier t n'est autre que Tr(M).
Comme l'a dit abcd22, les racines de ce polynôme sont des racines de l'unité.
Si ces racines sont réelles, il s'agit de 1 (racine double) ou -1 (racine double) mais pas -1 et 1 sinon le déterminant vaudrait -1. Dans le premier cas M est d'ordre 1, dans le second cas elle est d'ordre 2 (il s'agit de l'ordre au sens de l'ordre d'un élément du groupe SL2(Z) et pas de l'ordre de la matrice au sens de la taille de la matrice : il y a eu confusion dans un message plus haut).
Si ces racines sont non réelles, elles s'écrivent et
et  .
.
On a , mais t est un entier donc t est l'un des entiers 1, -1, 2, -2, et donc ces racines sont -j et -j², ou j et j², ou
, mais t est un entier donc t est l'un des entiers 1, -1, 2, -2, et donc ces racines sont -j et -j², ou j et j², ou
i et -i.
Le polynôme caractéristique est donc X²+1 ou X²-X+1 ou X²+X+1, et ces polynômes divisent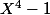 ou
ou 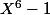 .
.
Comme l'a dit abcd22, les racines de ce polynôme sont des racines de l'unité.
Si ces racines sont réelles, il s'agit de 1 (racine double) ou -1 (racine double) mais pas -1 et 1 sinon le déterminant vaudrait -1. Dans le premier cas M est d'ordre 1, dans le second cas elle est d'ordre 2 (il s'agit de l'ordre au sens de l'ordre d'un élément du groupe SL2(Z) et pas de l'ordre de la matrice au sens de la taille de la matrice : il y a eu confusion dans un message plus haut).
Si ces racines sont non réelles, elles s'écrivent
On a
i et -i.
Le polynôme caractéristique est donc X²+1 ou X²-X+1 ou X²+X+1, et ces polynômes divisent
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
