Bonjour à tous,
J'ai une suite définie par u1>0 et un+1=1/(n*exp(un)).
J'ai prouvé que un tend vers 0 et je dois prouver que (un) est décroissante à partir d'un certain rang.
Avez-vous des idées ?
Merci.
Suite décroissante
11 messages
- Page 1 sur 1
Re: suite décroissante
Qu'as-tu essayé de faire ?
Tu connais les méthodes classiques pour montrer la décroissance d'une suite ?
(Tu peux t'aider de ce que tu as déjà montré)
Tu connais les méthodes classiques pour montrer la décroissance d'une suite ?
(Tu peux t'aider de ce que tu as déjà montré)
Re: suite décroissante
Bonjour
C'est assez étonnant que tu aies démontré que (u_n) cv vers zéro (ou alors tu as une démo un peu particulière) car le fait que la suite (u_n) est décroissante à partir de n=2 est une conséquence immédiate.
On a) pour tout n>1.
pour tout n>1.
Donc /(n e^{u_n})<1.)
C'est assez étonnant que tu aies démontré que (u_n) cv vers zéro (ou alors tu as une démo un peu particulière) car le fait que la suite (u_n) est décroissante à partir de n=2 est une conséquence immédiate.
On a
Donc
Re: suite décroissante
Bonjour Aviateur et merci !
J'ai bien prouvé un<1/(n-1), mais cela donne un+1/un>... donc ça ne marche pas comme cela.
J'ai bien constaté sur des tas d'exemples que j'ai programmés que la suite est décroissante à partir de n=2, mais la preuve me file entre les doigts chaque fois que je tente quelque chose.
Benoît
J'ai bien prouvé un<1/(n-1), mais cela donne un+1/un>... donc ça ne marche pas comme cela.
J'ai bien constaté sur des tas d'exemples que j'ai programmés que la suite est décroissante à partir de n=2, mais la preuve me file entre les doigts chaque fois que je tente quelque chose.
Benoît
Re: suite décroissante
Bonjour,
Aviateur vient de te donner la solution :
Pour montrer que la suite est décroissante, tu montre que u(n+1)/u(n)<1, et c'est ce qu'il a fait en utilisant u(n)<1/(n-1)
Aviateur vient de te donner la solution :
Pour montrer que la suite est décroissante, tu montre que u(n+1)/u(n)<1, et c'est ce qu'il a fait en utilisant u(n)<1/(n-1)
Re: suite décroissante
Salut,
Perso., sauf astuce que je ne vois pas, je suis d'accord avec BenoîtL-21 : la majoration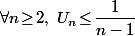 n'est pas suffisante pour conclure.
n'est pas suffisante pour conclure.
Par contre, en "poussant un cran plus loin", ça risque de marcher :
Pour tout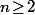 , on a
, on a \!\leq\exp\big(\frac{1}{n-1}\big)) donc
donc }\geq \dfrac{1}{n\,\exp\big(\frac{1}{n-1}\big)})
Ce qui signifie que\,\exp\big(\frac{1}{n-2}\big)}\ (*)) .
.
Ensuite, pour tout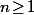 , on a les équivalences :
, on a les équivalences :
}\!\leq\!U_n\ \Leftrightarrow\ 1\!\leq n\,U_n \exp(U_n))
Et, vu l'inégalité (*), pour montrer un tel résultat pour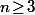 , il suffit (*) de montrer que
, il suffit (*) de montrer que
\,\exp\big(\frac{1}{n-2}\big)}{\blue \exp\bigg(\dfrac{1}{(n\!-\!1)\,\exp\big(\frac{1}{n-2}\big)}\bigg)}\geq 1)
Ce qui semble faisable (éventuellement via une ou des études de fonctions).
Vu la complexité de cette dernière formule, on se dit que ça serait pas con de faire plus simple, mais je vois pas trop comment procéder...
(*) Ce n'est pas un "il faut et il suffit", mais vu que la minoration (*) est "assez précise", ça serait étonnant que ça marche pas avec cette minoration là.
EDIT : en regardant de plus prés, ça se fait bien et la "grosse exponentielle" (en bleu), en fait, on peut se contenter de dire qu'elle est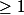 vu qu'on arrive à montrer que, pour
vu qu'on arrive à montrer que, pour  assez grand,
assez grand, 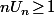 .
.
Perso., sauf astuce que je ne vois pas, je suis d'accord avec BenoîtL-21 : la majoration
Par contre, en "poussant un cran plus loin", ça risque de marcher :
Pour tout
Ce qui signifie que
Ensuite, pour tout
Et, vu l'inégalité (*), pour montrer un tel résultat pour
Ce qui semble faisable (éventuellement via une ou des études de fonctions).
Vu la complexité de cette dernière formule, on se dit que ça serait pas con de faire plus simple, mais je vois pas trop comment procéder...
(*) Ce n'est pas un "il faut et il suffit", mais vu que la minoration (*) est "assez précise", ça serait étonnant que ça marche pas avec cette minoration là.
EDIT : en regardant de plus prés, ça se fait bien et la "grosse exponentielle" (en bleu), en fait, on peut se contenter de dire qu'elle est
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: suite décroissante
Bonjour
Ok je me suis trompé. Grosse erreur d'étourderie: La majoration de u_n ne permet pas de majorer
 !!!
!!!
Ok je me suis trompé. Grosse erreur d'étourderie: La majoration de u_n ne permet pas de majorer
Re: suite décroissante
Rebjr, sur des exemples on conjecture que la suite est décroissante et "assez vite" mais cependant pas forcément à partir du rang 2.
Or on demande de montrer que la suite est décroissante à partir d'un certain rang (peu importe la connaissance du rang). Alors je propose cette démonstration qui ne demande qu'un petit calcul:
On sait déjà que cv vers 0 i.e
cv vers 0 i.e )
On a donc)=1/n+o(1/n))
On a donc.) Et on réinjecte ça dans
Et on réinjecte ça dans  :
:
}=1/n\times (1-1/n+o(1/n))=1/n-1/n^2+o(1/n^2))
on a donc-1/(n-1)^2+o(1/n^2))
Mais=1/n+1/n^2 + o(1/n^2)) (et
(et ^2=1/n^2+o(1/n^2)) )
)
donc)
On en déduit alors]-[1/n+o(1/n^2)]=-1/n^2+o(1/n^2))
Ce qui montre qu'à partir d'un certain rang
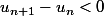 ,
,
c'est à dire que la suite est décroissante à partir d'un certain rang.
Or on demande de montrer que la suite est décroissante à partir d'un certain rang (peu importe la connaissance du rang). Alors je propose cette démonstration qui ne demande qu'un petit calcul:
On sait déjà que
On a donc
On a donc
on a donc
Mais
donc
On en déduit alors
Ce qui montre qu'à partir d'un certain rang
c'est à dire que la suite est décroissante à partir d'un certain rang.
Modifié en dernier par aviateur le 10 Oct 2018, 06:05, modifié 3 fois.
Re: suite décroissante
Heuuuuuu....aviateur a écrit:
Je suis pas bien convaincu que, quand on développe, le produit des termes en rouge donne un O(1/n)...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: suite décroissante
Effectivement, il y a de quoi ne pas être convaincu. En fait le o(1) et un o(1/n) obtenu en réinjectant un o(1) dans  ce que j'ai oublié de faire.
ce que j'ai oublié de faire.
En fait on a u_n=1/n+o(1/n) puis ensuite u_n=1/n+o(1/n^2).
Alors je corrige en bleu. Je modifie la fin aussi (différence à la place du quotient) . La différence étant plus pratique ici.
En fait on a u_n=1/n+o(1/n) puis ensuite u_n=1/n+o(1/n^2).
Alors je corrige en bleu. Je modifie la fin aussi (différence à la place du quotient) . La différence étant plus pratique ici.
Re: suite décroissante
Bon d'abord merci à tous de vous être penchés sur mon problème!!!
En effet la solution d'aviateur finit par marcher : en réinjectant u_n=1/n+O(1/n²) (ce que j'ai déjà prouvé) dans u_n+1, on obtient bien u_n=1/n+o(1/n²) (ou même +O(1/n^3). Puis en réinjectant cela dans u-n+1 - u_n : -1/n²+o(1/n²) d'où la négativité à partir d'un certain rang et la décroissance idem.
Dans la pratique, cela a l'air de se mettre à décroître très vite, mais peut-être qu'en choisissant bien u_1, cela peut ne se produire qu'à partir du rang 3 ou 4.
Super ! Merci beaucoup à tous !! Il y a un bon moment que je m'arrache les cheveux là-dessus.
En effet la solution d'aviateur finit par marcher : en réinjectant u_n=1/n+O(1/n²) (ce que j'ai déjà prouvé) dans u_n+1, on obtient bien u_n=1/n+o(1/n²) (ou même +O(1/n^3). Puis en réinjectant cela dans u-n+1 - u_n : -1/n²+o(1/n²) d'où la négativité à partir d'un certain rang et la décroissance idem.
Dans la pratique, cela a l'air de se mettre à décroître très vite, mais peut-être qu'en choisissant bien u_1, cela peut ne se produire qu'à partir du rang 3 ou 4.
Super ! Merci beaucoup à tous !! Il y a un bon moment que je m'arrache les cheveux là-dessus.
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
