Bonjour
La différence entre ce que je propose et ce que propose @ben la voici.
Mais d'abord ce qu'il y a de commun c'est que A(1)=R(1), A(2)= R(2) et A'(1)=R'(1) (dc 3 équations) .
Une fois que tu sais cela c'est simple: tu as un polynôme R a chercher dans un espace de dim 3.
1. Classiquement tu peux chercher la solution dans une base de cette espace et la base la première qui vient à l'esprit c'est la base canonique. C'est à dire que tu poses
=a \times 1 + b \times X + c\times X^2.)
Tu as donc 3 équations et 3 inconnues à résoudre et tu peux le refaire en exercice.
C'est la méthode que propose @ben et bien sûr il faut y penser.
Le prix à payer c'est de résoudre un système.
2. Maintenant comme toujours en algèbre linéaire tu peux changer de base de façon à ne pas avoir de système à résoudre si possible. C'est la méthode que je propose. Mais il y a un prix à payer c'est de trouver cette base.
Sans aller plus loin cette base, tu peux la deviner un peu par toi même ou penser avec l 'interpolation polynomiale de Lagrange et d'Hermite.
Remarque cette façon de procéder est surtout intéressante si ton reste est de degré assez élevé.
En effet si je je demande le reste de
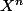
par A(x)=(x-1)(x-2),.....(x-10) tu vas te retrouver
avec un système 10x10 qui a tout les chances d'être horrible à résoudre alors qu'avec la seconde méthode
le résultat est (quasi) immédiat.
En résumé effectivement il faut d'abord comprendre la méthode de @ben.
Modifié en dernier par aviateur le 19 Aoû 2018, 16:24, modifié 3 fois.
?