Suite et complexes

[Chimarchalo]

Le V signe racine

(Zn) est la suite de nombres complexes definie par Zo = 1 et pour tout nombre entier naturel n, Zn+1 = (1+i(V3/3)) Zn dans le plan complexe on note An le point d’affixe Zn

1) a) placer Ao, A1, A2, et A3
b) determinier la forme exponentielle de 1 + i(V3/3)
c) montrer que pour tout nombre entier naturel n, Zn = (2/V3)^n e^in pi/6

2) pour tout nombre entier naturel n on pose : dn = |Zn+1 - Zn|

a) demontrer que la suite (dn) est géométrique
b) demintrer que pour tout nombre entier naturel n |Zn+1|^2 = |Zn|^2 + dn^2
c) en déduire que, pour tout nombre entier naturel n, le triangle OAnAn+1 est rectangle en An

[capitaine nuggets]

Bonjour à toi aussi...
C'est toujours la même chose, qu'as-tu fait ? Où bloques-tu ?

1.a) Il suffit de connaître , , 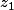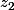et 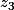, rien de bien difficile.
b) On calcule le module et un argument de .
c) On peut raisonner par récurrence.

2.a) Ca se montre directement à partir de la définition par récurrence de (pas besoin d'utiliser la question 1.c).
b) Tu peux par exemple utiliser 1.c)
c) C'est le théorème de Pythagore.

[Chimarchalo]

Bonsoir, désolé, et merci de m’avoir joint les documents (liens) ,
Je ne parviens pas a effectuer le raisonnement pas recurence une fois l’initialisation faite l’hypothèse de récurrence et le développement me bloque (question 1c)

[Pseuda]

Question 1c : c'est plus simple que ça, ce n'est pas une récurrence, on met un nombre complexe exprimé sous forme exponentielle à la puissance : le module devient ? l'argument devient ?

[capitaine nuggets]

Salut !

J'avoue, je devais être fatigué mdr...
Évidemment, d'après l'énoncé est une suite géométrique de premier terme 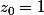et de raison (forme exponentielle de d'après 1.b)) donc . C'est immédiat puisque le travail a été fait en 1.b).