Les questions de Théo

[Théo3401]

Bonjour à tous !
Toujours sur la trigo, j'ai à nouveau besoin de votre aide :

Je dois exprimer les fonctions suivantes sous la forme t=f(s) :

s=3.sin(2t + pi/2)

j'arrive au point :
(sin(t))^2 = 1/2 . ((-s+3)/3)

Aussi si quelqu'un peut m'aider à résoudre mon problème d'éditeur d'équation ce serait cool !
Je ne sais pas pourquoi ça ne fonctionne pas, je click sur "insérer dans la zone de texte" mais rien ne se passe.


Merci d'avance à tous !!

Théo

[Ben314]

Salut,
Si que tu appelle "un éditeur d'équation", c'est le MimeTeX utilisé sur le Forum, il y a une doc (succincte mais bien faite) là :
guide-utilisation-f41/bonne-utilisation-des-parentheses-t118463.html
Une autre méthode pas con, c'est de "citer" les messages des autres pour voir comment ils ont codés leurs formules.

Sinon, ça :

Je dois exprimer les fonctions suivantes sous la forme t=f(s) :
s=3.sin(2t + pi/2)

c'est clairement impossible : la fonction est périodique (de période ) donc si tu te donne un fixé et que tu cherche à résoudre il y aura soit aucune solution, soit une infinité et dans les deux cas, il est évidement impossible d'écrire un truc du style .
Dit avec des mots plus compliqués, ton truc ça consiste à chercher la bijection réciproque de , sauf que n'est absolument pas bijective, donc c'est voué à l'échec.

[Théo3401]

Alors je ne suis pas trop sur si c'est moi qui ai mal expliqué ce que je cherchais à résoudre.
Mais nous avons fais la correction aujourd'hui et s = 3.sin(2.t + (pi/2)
<=>s/3 = sin(2t+(pi/2))
<=>arcsin(s/3) = 2.t + (pi/2)
<=>arcsin(s/3)-(pi/2) = 2t
<=> t = (1/2).arcsin(s/3) - (pi/2)


Merci pour votre aide

Théo

[Ben314]

s/3 = sin(2t+(pi/2))
<=>arcsin(s/3) = 2.t + (pi/2)

Sauf que ça, c'est complètement faux : A=sin(B) n'est pas du tout équivalent à arcsin(A)=B.
Ce n'est vrai que si on sait à l'avance que B est entre -pi/2 et pi/2 mais sans aucune information sur B, tout ce qu'on peut dire, c'est que A=sin(B), c'est équivalent à B=arcsin(A)+2k.pi avec k dans Z ou bien B=pi-arcsin(A)+2k.pi avec k dans Z. Donc une infinité des solutions.
C'est très exactement la même chose que le fait que A=B^2 ce n'est pas équivalent à racine(A)=B : Si A est positif, l'équation (d'inconnue B) A=B^2 admet deux solutions : B=racine(A) et B=-racine(A).
Par exemple X^2=4 a comme solutions X=2 et X=-2. C'est un "piège" qu'on apprend normalement à éviter dés le collège.

Donc la "correction" est fausse et tu peut le vérifier sur des tonne d'exemples :
- Si on prend par exemple t=pi alors la formule s = 3.sin(2.t + pi/2) donne s=3
- Alors que si on prend s=3, la formule t = (1/2).[arcsin(s/3) - pi/2] donne t=0 différent du t=pi de départ.

Sans indiscrétion, c'est qui qui t'a proposé ça comme "correction" ?

[Théo3401]

ahaha tu vas adorer.... : Mon prof qui est soit dit en passant physicien théoricien de ses dires
Merci pour tes explications, j'ai bien compris la raison de pourquoi tu disais que c'était impossible (les exemples ont bien aidé)
Merci pour ton temps Ben314 !

[Théo3401]

Bonjour à tous !
Premièrement, je voulais savoir si quelqu'un aurait une solution à mon problème : Je ne peux pas me servir de l'éditeur d'équation. C'est à dire que je peux la tapper, puis des que je met inserer dans la zone de texte, rien ne se passe.

Je passe maintenant à ma question, que je ne pourrais malheureusement pas vous montrer avec cette fonction qu'offre le site :

Je cherche la primitive de { 1/(cos^2(7x) } afin d'en trouver l'integrale.
Une idée de piste??

Merci d'avance,

Théo

[Elias]

Salut,
Ça serait pas mal de préciser les bornes de l'intégrale que tu souhaites calculer (déjà pour voir si la fonction x -> 1/cos^2(7x) est bien définie).

Ceci étant dit, cherche la dérivée de la fonction tangente et ça va te débloquer.

Et puis, il n'y a pas UNE SEULE primitive mais une infinité donc tu cherches plutôt une primitive et pas LA primitive.

PS: si tu veux faire apparaître , il faut taper :

Code: Tout sélectionner

[tex]x \mapsto \frac{1}{cos^2(7x)}[/tex]

[Ben314]

Salut,
Bon, déjà, tu cherche pas LA primitive de . . . mais UNE primitive de . . . (il est absolument indispensable de distinguer les choses "uniques" de celles qui ne le sont pas en math. sinon tu va rapidement écrire d'énormes conneries)
Ensuite, sans réfléchir plus loin que le bout de mon nez, la méthode "bétassous" dans des cas pareil d'intégrale de fonction trigonométriques, c'est de poser qui donne ; et (formule archi classiques).
Sinon, en réfléchissant un peu plus (et en tenant compte de la forme du truc à intégrer), il y a des fois des changement de variable qui donnent des trucs plus simple. Par exemple ici,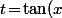 suffit.

P.S.1 : évidement, tout ça en commençant par virer le 7 du cos(7x) à l'aide d'un premier changement de variable.

P.S.2. :

Code: Tout sélectionner

[tex]x \mapsto \frac{1}{cos^2(7x)}[/tex]

Avec \cos (avec un backslash), c'est plus joli et plus standard... (et \dfrac à la place de \frac pour qu'on voit mieux la différence) :
[tex]x \mapsto \dfrac{1}{cos^2(7x)}[/tex] ->
[tex]x \mapsto \dfrac{1}{\cos^2(7x)}[/tex] ->

[Théo3401]

Super Ben ! Merci beaucoup pour ton aide, j'ai réussi, cet exercice grace à toi, et je continue de chercher LES primitives des prochains exercices
(C'était une erreur d'inattention de ma part, mais juste pour être sur, on parle de chercher DES primitives car il y a cette constance C/k?)

Merci encore !

Théo

[Ben314]

Je suis pas super balèse en Français, mais a mon sens concernant le mot "primitives" :
- Soit on cherche UNE primitive vu qu'on a juste besoin de ça (par exemple pour calculer une intégrale)
- Soit on cherche l'ensemble de toutes LES primitives de la fonction en question.
Mais de chercher DES primitives, je vois pas bien l'intérêt...

Bon, après, dans le cas des primitives, en chercher une ou bien les chercher toutes, ça fait pas une grosse différence vu que sur un intervalle donné, toutes les primitives s'obtiennent en partant d'une primitive et en ajoutant une constante arbitraire.

[Théo3401]

Merci ben ! et désolé Trident j'avais complètement raté ta réponse.
Bon aujourd'hui je passse ma journée à la médiathèque je vais donc être assez actif sur le forum.
Enfaite j'ai refait tous les exercices qui se trouvent dans les chapitres Intégrales et Dérivées.

Ca c'est plutôt bien passé, à part pour quelque uns pour les quels j'ai besoin de votre aide ou de votre lumière

Le premier problème que j'ai se trouve surtout dans la non compréhension de l'énoncé (me semble t-il).



La réponse donné dans le bouquin étant 2 (je vous ai mis une photo plutot que d'utiliser l'éditeur d'équation pour que vous voyez un peu comment l'énoncé est foutu)

Donc pour moi il est tout à faire logique que , en revanche, ...

Merci d'avance, pour ne pas vous submerger de question j'attendrais que quelqu'un ai la gentillesse de me répondre avant de poster la prochaine.

Bien a vous tous,

Théo

[Elias]

Salut,

tu soulèves une question qui fait l'objet de quelques débats. Ben314 va sans doute mieux te répondre et apporter plus de précisions que moi.

Mais ici, je dirais que l'auteur doit considérer la limite dite épointée.

Autrement dit, on a ici mais on ne peut pas dire que

En effet, écrire signifie que pour tout 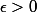, il existe 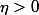tel que pour tout réel,


Or, lorsque est assez petit (précisément, plus petit que 3), on ne peut pas dire que ce qui est écrit ci-dessus est vrai puisque c'est pas vrai avec .

Ecrire en revanche signifie que 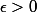, il existe 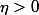tel que pour tout réel,, ce qui est vrai cette fois-ci.

[Ben314]

Sur ces histoires de limites "épointées", effectivement, il y a plus ou moins un "bug" dans la façon de voire les choses en France (je pense qu'on est les seul à raisonner comme ça).
Dans la définition de limite d'une fonction (avec le epsilon et le éta) donnée à peu prés partout en France, effectivement rien ne précise que le x doit être distinct du xo alors que dans la plupart des autres pays, c'est le cas (donc si l'énoncé à été pioché sur un truc au départ non Français, ça va pas coller...)
Et cette histoire de limite "non épointée" en Français, là où c'est pas mal con, c'est pour la définition de continuité vu que de dire que f(xo) = lim f(x) lorsque x->xo, c'est on ne peut plus couillon vu qu'avec une définition "non épointé", ben si la limite en question existe (et que f(xo) aussi), alors elle est forcément égale à f(xo).

Bref, quand tu voit du dans un énoncé, il faut toujours se poser la question de savoir si l'auteur à bien voulu dire exactement ça (avec la définition Française non épointé) ou si par hasard, il n'aurait pas voulu dire .

Et là, l'exercice en question, il est "caricatural" concernant ce problème de définition.

[Pseuda]

Bonsoir,

En résumé, avec la définition de la limite "épointée", la limite de f en 1 est 2, et avec la définition "non épointée" (la version française), la fonction n'a pas de limite en 1.
Dans les 2 cas, la fonction n'est pas continue en 1. Dans le 1er cas, parce que sa limite n'est pas égale à f(1)=5, dans le 2ème cas, parce qu'elle n'a pas de limite en 1.

Perso, je trouve la définition hors France beaucoup plus claire (décidément on aime se compliquer). Une limite, c'est une limite, ce n'est pas une égalité. Mais d'autres considérations doivent certainement m'échapper. Mais c'est vrai que du coup, on se pose la question à chaque fois.

[Théo3401]

Merci à tous les deux pour vos réponse !
Je vous écris de Bruxelles, donc apparement le problème est le même ici en Belgique.

Merci encore,

Théo