Analyse complexe

[manelrj]

bonsoir a tous est ce que vous pouvez m'aider de savoir pourquoi une fonction holomorphe de classe C1 est de classe infini ???

[Ben314]

Salut,
En fait, tu as même pas besoin de C^1 : une fonction (à valeur complexe) définie et C-dérivable (c'est à dire holomorphe) sur un ouvert U de C est forcément C^oo et même analytique (ce qui est pas mal plus fort que C^oo) sur U.

Et la preuve, ben en général, ça fait (quasiment) l'objet d'un chapitre entier sur le cours sur les fonctions holomorphes (éventuellement appelé cours sur les fonctions analytiques...)
En général, on procède de la façon suivante :
- On démontre le théorème des triangles de Goursat.
- On en déduit le théorème intégral de Cauchy (ou uniquement une version plus faible ne concernant que les cercles)
- On montre grâce à ça que, si on prend un disque (fermé) centré en 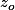alors, pour tout dans l’intérieur de , on a .
- On en déduit par les théorèmes classiques d'interversion somme/intégrale que, pour tout dans l’intérieur de , on a avec
Ce qui prouve que est analytique (donc C^oo) sur l’intérieur de et que

Dans le cas où on suppose au départ que f est C^1 (et pas seulement holomorphe), il y a des variantes légèrement plus rapide qui évitent le passage par le théorème des triangle de Goursat pour montrer directement le théorème intégral de Cauchy (perso, je trouve que c'est un peu con : on gagne pas plus d'une petite heure dans le cours pour un résultat moins joli. Mais bon, ce n'est qu'un avis et ça dépend évidement du temps disponible...)