Bonjour à tous, voici mon exo tiré du concours bécéas 2O16.
J'ai vraiment besoin de votre aide pour résoudre cette partie:
Calcul de
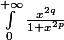
a) Soit A un réel strictement positif et

une fonction continue sur

à valeurs dans

dont on note

(resp.

) la partie réelle (resp. imaginaire).
On rappelle (ou on admet) que
dt})
désigne la somme
dt{})
+
dt})
Doit
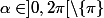
Etabilir l'égalité
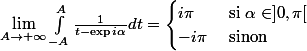
b) On note pour tout
i\pi}{2p}))
Etalir pour tout
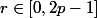
, l'existence et l'unicité du polynôme de
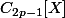
, noté
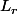
tel que
=\begin{cases} 0 & \text{ si } k\neq r \\ -i\pi & \text{ sinon } \end{cases})
c) soit
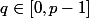
Justifier l'existence de nombres complexes
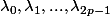
tel que pour tout réel t,
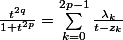
Merci déjà!
