Suites arithmétiques et géométriques

[Oriane2000]

Bonjour à tous,


(Un) est une suite arithmetique definie sur N.
Montrer que la suite (Vn) définie pour tout n appartient à N par Vn(indice Un) est une suite géométrique et preciser sa raison.

Pouvez vous m'aider sur cet exercie svp, je suppose qu'il faut utiliser la formule Un+1 / Un = q
Et Un+1 - Un = r mais je ne parviens pas à calculer, merci à tous bonne journée

[Mimosa]

Bonjour

Ton énoncé cloche! Si on prend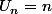 on a bien une suite arithmétique, mais alors n'est certainement pas géométrique!

[annick]

Bonjour,
pourrais-tu nous donner ton énoncé en entier car là, il semble manquer beaucoup de choses.

[pascal16]

Vn=k exposant Un pourrait marcher

[Oriane2000]

Ah oui excusez moi jai oublie cela : Vn = 2 (indice Un)
Maintenant l'énoncé est au complet

[Oriane2000]

Qqn peut il m'aider svp ?

[pascal16]

Vn = 2 (indice Un)
c'est plutôt 2 exposant Un soit
tu peux essayer l'éditeur d'équations , le code est : 2^{U_n}
^ : c'est pour l'exposant
{} : c'est comme des parenthèses invisibles pour grouper des termes
U_n, le _ crée l'indice

on y va :
Un arithmétique, donc, il existe Uo et r tel que : Un= Uo+ n r
ensuite, vas-y façon bourrin , on calcule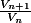
( code pour l'écrire : \frac{V_{n+1}}{V_n} )
si on trouve une constante, Vn est géométrique.

[Oriane2000]

Merci c'est bien pratique l'éditeur d'équation !






Seulement après voila que je bloque ... La formule nous permet d'obtenir la raison , mais je ne vois pas comment montrer sa constance, ni le rapport avec le fait de prouver que la suite est géométrique ... Je vous prie de m'excuser j'ai un peu de mal avec ce chapitre ...

[pascal16]

rappel




est donc constant car r est un nombre fixe, donc 2^r l'est aussi

[narukira]

Bonjour à tous,


(Un) est une suite arithmetique definie sur N.
Montrer que la suite (Vn) définie pour tout n appartient à N par Vn(indice Un) est une suite géométrique et preciser sa raison.

Pouvez vous m'aider sur cet exercie svp, je suppose qu'il faut utiliser la formule Un+1 / Un = q
Et Un+1 - Un = r mais je ne parviens pas à calculer, merci à tous bonne journée

Bjr comment est Un?

[Oriane2000]

Ahh merci ! Un est arithmétique donc on trouve bien 2^r
Donc 2^r est la raison de Vn est ce bien cela ?

[pascal16]

oui

[Oriane2000]

Merci bcp