Bonjour,
je me suis posé une question et je n'ai pas trouvé la réponse après de rapides recherches:
Comment calculer la probabilité de tirer n éléments tous différents, avec X tirages aléatoires, sachant que l'on peut tirer plusieurs fois le même élément. Les n issues sont équiprobables. Si je me suis mal exprimé, voici le problème concret:
Il existe une collection de 30 cartes de jeu, quelle est la probabilité en fonction de X de compléter le jeu en tirant une carte aléatoire X fois sachant que chaque carte a la même probabilité d'être tirée et que l'on peut tirer plusieurs fois la même carte?
Merci d'avance
Note: Je sais déjà que le nombre moyen de tirages pour compléter le jeu est de 30*ln(30) mais je cherche la probabilité de compléter le jeu en fonction de X, donc une sorte de suite croissante et qui est égale à 1 quand X tend vers l'infini.
Probabilité: problème du collectionneur
3 messages
- Page 1 sur 1
Re: Probabilité: problème du collectionneur
Salut,
Y'a effectivement une formule théorique générale, mais elle utilise un truc moyennement connu.
Lorsque tu effectue tirages (avec remise) dans un ensemble de
tirages (avec remise) dans un ensemble de  cartes, la proba que tu ait en ait tiré exactement
cartes, la proba que tu ait en ait tiré exactement  différentes est :
différentes est :
\dfrac{c(c\!-\!1)(c\!-\!2)...(c\!-\!k\!+\!1)}{c^n})
où les) sont les nombres de Stirling de seconde espèce.
sont les nombres de Stirling de seconde espèce.
Vu que dans ton problème, tu t'intéresse uniquement au cas où est fixe (égal à
est fixe (égal à  lui même égal à 30), tu peut éventuellement utiliser le fait que
lui même égal à 30), tu peut éventuellement utiliser le fait que
\!=\!\dfrac{1}{k!}\sum_{i=0}^k(-1)^{k-i}\begin{pmatrix}k\\ i\end{pmatrix}i^n)
où les!}) sont les coefficients binomiaux.
sont les coefficients binomiaux.
Ca te donne :
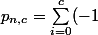^{i}\begin{pmatrix}c\\ i\end{pmatrix}\Big(\dfrac{c\!-\!i}{c}\Big)^n)
Y'a effectivement une formule théorique générale, mais elle utilise un truc moyennement connu.
Lorsque tu effectue
où les
Vu que dans ton problème, tu t'intéresse uniquement au cas où
où les
Ca te donne :
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Probabilité: problème du collectionneur
Bonjour,
Je n'ai pas encore vu les coefficients binomiaux mais d'après tes informations, j'ai remplacé les inconnues dans la dernière expression:
Somme[(-1)^i*((30!)/(i!*(30-i)!))*((30-i)/30)^n, i, 0, 30]
donc la variable est n. j'en ai fait une fonction même si c'est stupide vu que n est entier et j'obtiens ça
Ce qui me semble plutôt cohérent.
Merci beaucoup pour ton aide j'ai compris
Je n'ai pas encore vu les coefficients binomiaux mais d'après tes informations, j'ai remplacé les inconnues dans la dernière expression:
Somme[(-1)^i*((30!)/(i!*(30-i)!))*((30-i)/30)^n, i, 0, 30]
donc la variable est n. j'en ai fait une fonction même si c'est stupide vu que n est entier et j'obtiens ça

Ce qui me semble plutôt cohérent.
Merci beaucoup pour ton aide j'ai compris
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
