Bonjour,
U est l'univers (fini) d'une expérience aléatoire. Je ne comprends pas quel est le lien entre loi de probabilité sur U et probabilité sur U. De même, j'aimerais que quelqu'un m'explique ce que c'est concrètement (je suis en 1ère) un espace probabilisable, un espace probabilisé et une tribu d’événements.
Merci d'avance pour vos réponses.
Probabilité et loi de probabilité
8 messages
- Page 1 sur 1
Re: Probabilité et loi de probabilité
Une probabilité sur U (dans la suite U est un ensemble fini ou dénombrable comme 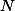 par exemple) est une application de l'ensemble des événements de U dans [0,1] qui vérifie quelques axiomes :
par exemple) est une application de l'ensemble des événements de U dans [0,1] qui vérifie quelques axiomes :
=1)
Si_{n\in\mathbb{N}}) est une suite d'événements deux à deux disjoints, alors
est une suite d'événements deux à deux disjoints, alors 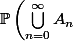=\sum_{n=0}^{+\infty}\mathbb{P}(A_n))
Depuis le début je parle d'événement sans avoir dit ce que c'est : un espace probabilisé est un espace) où U est l'univers des possibles,
où U est l'univers des possibles,  l'ensemble des événements (c'est un ensemble de sous-ensembles de U) et
l'ensemble des événements (c'est un ensemble de sous-ensembles de U) et 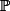 la probabilité, un espace
la probabilité, un espace ) est dit probabilisable si on peut lui associer une probabilité. L'ensemble
est dit probabilisable si on peut lui associer une probabilité. L'ensemble  est une tribu par défintion, c'est à dire qu'elle est non vide, elle est stable par complémentaire et stable par réunion dénombrable :
est une tribu par défintion, c'est à dire qu'elle est non vide, elle est stable par complémentaire et stable par réunion dénombrable :
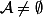
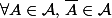
Si_{n\in\mathbb{N}}) est une suite d'éléments de
est une suite d'éléments de  alors
alors 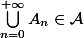
Ce que je viens de te dire n'est pas du tout au programme de 1ère d'ailleurs.
Si
Depuis le début je parle d'événement sans avoir dit ce que c'est : un espace probabilisé est un espace
Si
Ce que je viens de te dire n'est pas du tout au programme de 1ère d'ailleurs.
Re: Probabilité et loi de probabilité
Ok, mais quel est le lien entre loi de probabilité sur U et probabilité sur U?
Merci Tuvasbien pour ta réponse.
Merci Tuvasbien pour ta réponse.
Re: Probabilité et loi de probabilité
Mais on devrait pas plutôt dire probabilité sur P(U) (ensemble des événements) au lieu de probabilité sur U puisque on associe un réel compris entre 0 et 1 à chaque événement?
Re: Probabilité et loi de probabilité
Le problème c'est que la loi de probabilité est définie sur la tribu de l'espace probabilisé ) et donc la loi de probabilité ne dépend pas que de U et à priori, les éléments de
et donc la loi de probabilité ne dépend pas que de U et à priori, les éléments de ) ne sont pas tous des événements (il peut exister des ensembles un peu tordus qui ne sont pas mesurables). Sur un espace probabilisé fini les événements sont simplement les éléments de
ne sont pas tous des événements (il peut exister des ensembles un peu tordus qui ne sont pas mesurables). Sur un espace probabilisé fini les événements sont simplement les éléments de ) ce qui a toujours été le cas vu que tu es en 1ère.
ce qui a toujours été le cas vu que tu es en 1ère.
Re: Probabilité et loi de probabilité
Je suis perdu... oublions toutes les notions des tribus, en 1ère, on nous dit qu'une loi de probabilité est une application P qui va de U dans [0,1]. C'est-à-dire qu'on associe à chaque événement élémentaire un nombre compris entre 0 et 1. Mais, pour un événement constitué de plusieurs événements élémentaires, comment on fait pour calculer sa probabilité (la probabilité d'un événement est la somme des probabilités des éléments le constituant) car P ne fait qu'associer à un événement élémentaire. C'est un peu flou, j'espère que je me suis fait comprendre.
Et merci beaucoup Tuvasbien pour m'avoir répondu aussi vite.
Et merci beaucoup Tuvasbien pour m'avoir répondu aussi vite.
Re: Probabilité et loi de probabilité
Et bien c'est un mensonge ou plutôt un cas particulier plus simple de la définition (trop compliquée pour l'enseigner à des premières), c'est juste que dans le cadre d'un univers fini on considère que l'ensemble des événements possibles est ) . Par contre, je ne sais pas si c'est une faute de frappe mais une probabilité ne va pas de U dans [0,1] mais de
. Par contre, je ne sais pas si c'est une faute de frappe mais une probabilité ne va pas de U dans [0,1] mais de ) dans [0,1] de sorte que les événements triviaux sont des singletons. Par exemple si ton univers est
dans [0,1] de sorte que les événements triviaux sont des singletons. Par exemple si ton univers est 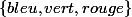 alors
alors ) n'a pas de sens mais
n'a pas de sens mais ) ou
ou ) oui. Si alors on veut calculer
oui. Si alors on veut calculer ) alors avec ta définition le calcul est
alors avec ta définition le calcul est =\mathbb{P}("rouge")+\mathbb{P}("vert")) . En fait ça provient de la vraie définition : pour toute suite d'événements deux à deux disjoints
. En fait ça provient de la vraie définition : pour toute suite d'événements deux à deux disjoints _{n\in\mathbb{N}},\ \mathbb{P}\left(\bigcup_{n=0}^{+\infty}{A_n}\right)=\sum_{n=0}^{\infty}{\mathbb{P}(A_n)}) . En fait
. En fait 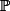 n'agit pas que sur les événements élémentaires mais sur tous les événements et les règles de calcul permettent de calculer des probabilités d'événement plus complexes que des événements triviaux.
n'agit pas que sur les événements élémentaires mais sur tous les événements et les règles de calcul permettent de calculer des probabilités d'événement plus complexes que des événements triviaux.
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
