Bonjour,
Voici l'énoncé :
"Montrer par récurrence que pour tout entier n≥1, 1^3+3^3+...+(2n-1)^3=2n^4-n^2
J'ai donc fait initialisation :
pour n=1
1^3+3^3+...+(2-1)^3=2^4-1^2
<=> 1+27+...+1=15
Je reconnais une suite arithmétique avec U(x)=x^3 mais je ne sais pas comment faire.
Dois-je faire la somme des termes pour trouver 15 ?
Merci de votre aide
Exercice récurrence
11 messages
- Page 1 sur 1
Re: Exercice récurrence
salut
l'initialisation est simplement : ...
...
l'initialisation est simplement :
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Exercice récurrence

si n = 1 alors 2n - 1 = 1
donc il n'y a qu'un seul terme dans la somme ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Exercice récurrence
Salut,
Cette expression là :
Là, ton truc, écrit en français, c'est "La somme des cubes des entiers impairs de 1 à 2n-1 (qui est bien impair)"
Et, lorsque n=1, ça veut dire que c'est "La somme des cubes des entiers impairs de 1 à 1" c'est à dire que c'est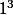 et c'est tout.
et c'est tout.
Et une autre façon de le voir, c'est ce que te dit zygo : ta somme, c'est^3\!+\!(2\!\times\!2\!-\!1)^3\!+\!(2\!\times\!3\!-\!1)^3\!+\!\cdots\!+\!(2\!\times\!n\!-\!1)^3) et elle contient donc
et elle contient donc  termes vu que c'est la somme des
termes vu que c'est la somme des ^3) où
où  va de 1 à
va de 1 à  )
)
Donc quand n=1, ben la somme elle contient 1 terme et c'est tout.
Cette expression là :
comme toute celle avec des points de suspension, elle est là pour donner "le principe" de la formule, mais elle est évidement à interpréter en fonction de n !!!JulienNv a écrit:1^3+3^3+...+(2n-1)^3
Là, ton truc, écrit en français, c'est "La somme des cubes des entiers impairs de 1 à 2n-1 (qui est bien impair)"
Et, lorsque n=1, ça veut dire que c'est "La somme des cubes des entiers impairs de 1 à 1" c'est à dire que c'est
Et une autre façon de le voir, c'est ce que te dit zygo : ta somme, c'est
Donc quand n=1, ben la somme elle contient 1 terme et c'est tout.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Exercice récurrence
Merci pour vos réponses
Donc si j'ai bien compris ensuite je fais l'hérédité :
-1)^3=2(p+1)^4-(p+1)^2)
J'ai donc compris que je dois démontrer que la somme des termes de 1 à-1)^3) est égale à
est égale à ^4-(p+1)^2)
Si je fais la somme des termes avec la formule a (1 − q^n ) / (1 − q ) je n'arrive pas a obtenir le bon résultat.
En développant les deux expressions j'ai quand même vus que-1)^3=8p^3+12p^2+6p+1) or
or ^4-(p+1)^2=2p^4+8p^3+12p^2+8p+2)
On obtient en faisant la différence je n'arrive pas a trouver les termes qui rajoutent cette valeur a la somme...
je n'arrive pas a trouver les termes qui rajoutent cette valeur a la somme...
Merci de votre aide
Donc si j'ai bien compris ensuite je fais l'hérédité :
J'ai donc compris que je dois démontrer que la somme des termes de 1 à
Si je fais la somme des termes avec la formule a (1 − q^n ) / (1 − q ) je n'arrive pas a obtenir le bon résultat.
En développant les deux expressions j'ai quand même vus que
On obtient en faisant la différence
Merci de votre aide
Re: Exercice récurrence
Si je fais la somme des termes avec la formule a (1 − q^n ) / (1 − q ) je n'arrive pas a obtenir le bon résultat.
il est clair qu'en utilisant une formule valable pour les suites géométriques à une suite qui n'est pas géométrique ça risque de merder !!!
ensuite pour l'hérédité il faudrait peut-être utiliser l'hypothèse de récurrence ...
et pour cela comme ben314 l'a déjà dit peut-être qu'à la place des points de suspension (ou en complément) il serait bien d 'écrire un peu plus de termes pour voir réellement les choses ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Exercice récurrence
certes oui ... mais c'est la fin qui m'intéresse : les trois derniers termes (et sans simplification)
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Exercice récurrence
hypothèse de récurrence :  \ : \ 1^3 + 2^3 + 3^3 + ... + (2n - 3)^3 + (2n - 1)^3 = 2n^4 - n^2)
^3 + (2n - 1)^3 + [2(n + 1) - 1]^3 = 2n^4 - n^2 + (2n + 1)^3 = ...)
développer pour obtenir^4 - (n + 1)^2)
...
développer pour obtenir
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
