Bonjour, j'ai un exercice sur les suites mais je bloques aux dernières questions..
On considère la suite (Un) définie par U0=-1
U1= 1/2
Un+2=Un+1-1/4Un
On note ensuite Sn=U0+U1+...Un, la somme des (n+1) premiers termes de la suite (Un).
Le but de cet exercice est de déterminer une expression de la somme Sn en fonction de n.
1.Calculer S3
J'ai calculé U2(=3/4) et U3(5/8) pour trouver S3=7/8
2. J'ai du analyser un algorithme
3. Prouver que la suite (Un) n'est ni arithmétique ni géométrique
J'ai fait u1-u0(=3/2) et u2-u1(=1/4) j'ai remarqué que le résultat n'était pas le même donc non arithmétique.
Ensuite j'ai fait u1/u0(=-1/2) et u2/u1(=3/4)) alors idem que précédemment.
4. On définit la suite (Vn) en posant pour tout entier naturel n : Vn=Un+1-(1/2Un)
a. Calculer V0
J'ai trouvé 1.
b.Montrer que (Vn) est une suite géométrique de raison q=1/2
C'est fait j'ai trouvé.
c. Exprimer Vn en fonction de n
Vn= 1*(1/2)^n
5. On définit la suite Wn=Vn/Un
a. Calculer Wo
J'ai trouvé -1.
b. C'est ici que je bloque
En utilisant l'égalité Un+1=Vn+(1/2Un), montrer que (Wn) est arithmétique de raison r=2
Alors j'ai commencé comme ceci:
Wn+1= Un+1/Vn+1
=> (Vn+(1/2Un))/Vn+1
=> (Vn+(1/2Un))/(1/2Vn)
Après j'ai essayé de remplacer Vn par Un+1-(1/2Un)ce qui m'a donné
(Un+1-(1/2Un)+(1/2Un))/(1/2)*(Un+1-(1/2)Un)
=> Un+1/(1/2)*(Un+1-(1/2)Un)
Et là je bloque .. Je ne sais plus comment faire..
6. Montrer que pour tout entier naturel n, on a : Un=(2n-1)/2^n
7.Montrer par récurrence que : Sn=2-(2n+3)/2^n
Ici j'ai commencé l'initialisation:
Initialisation: D'après l'énoncé on a S0=U0=-1
S0= 2-(2*0+3)/2^0
= -1
La propriété est vérifiée au rang n=0
Mais l'hérédité me bloque..
Merci d'avoir pris le temps de me lire.
Exercice sur les Suites, récurrence..
3 messages
- Page 1 sur 1
Eliabrcd a écrit:Bonjour, j'ai un exercice sur les suites mais je bloques aux dernières questions..
On considère la suite (Un) définie par U0=-1
U1= 1/2
Un+2=Un+1-1/4Un
On note ensuite Sn=U0+U1+...Un, la somme des (n+1) premiers termes de la suite (Un).
Le but de cet exercice est de déterminer une expression de la somme Sn en fonction de n.
1.Calculer S3
J'ai calculé U2(=3/4) et U3(5/8) pour trouver S3=7/8
2. J'ai du analyser un algorithme
3. Prouver que la suite (Un) n'est ni arithmétique ni géométrique
J'ai fait u1-u0(=3/2) et u2-u1(=1/4) j'ai remarqué que le résultat n'était pas le même donc non arithmétique.
Ensuite j'ai fait u1/u0(=-1/2) et u2/u1(=3/4)) alors idem que précédemment.
4. On définit la suite (Vn) en posant pour tout entier naturel n : Vn=Un+1-(1/2Un)
a. Calculer V0
J'ai trouvé 1.
b.Montrer que (Vn) est une suite géométrique de raison q=1/2
C'est fait j'ai trouvé.
c. Exprimer Vn en fonction de n
Vn= 1*(1/2)^n
5. On définit la suite Wn=Vn/Un
a. Calculer Wo
J'ai trouvé -1.
b. C'est ici que je bloque
En utilisant l'égalité Un+1=Vn+(1/2Un), montrer que (Wn) est arithmétique de raison r=2
Alors j'ai commencé comme ceci:
Wn+1= Un+1/Vn+1
=> (Vn+(1/2Un))/Vn+1
=> (Vn+(1/2Un))/(1/2Vn)
Après j'ai essayé de remplacer Vn par Un+1-(1/2Un)ce qui m'a donné
(Un+1-(1/2Un)+(1/2Un))/(1/2)*(Un+1-(1/2)Un)
=> Un+1/(1/2)*(Un+1-(1/2)Un)
Et là je bloque .. Je ne sais plus comment faire..
6. Montrer que pour tout entier naturel n, on a : Un=(2n-1)/2^n
7.Montrer par récurrence que : Sn=2-(2n+3)/2^n
Ici j'ai commencé l'initialisation:
Initialisation: D'après l'énoncé on a S0=U0=-1
S0= 2-(2*0+3)/2^0
= -1
La propriété est vérifiée au rang n=0
Mais l'hérédité me bloque..
Merci d'avoir pris le temps de me lire.
(Vn+(1/2Un))/(1/2Vn)
soit Wn+1=2+Un/Vn=2+Wn
Salut !
C'est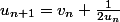 ou
ou 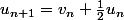 ?
?
Eliabrcd a écrit:5. On définit la suite Wn=Vn/Un
a. Calculer Wo
J'ai trouvé -1.
b. C'est ici que je bloque
En utilisant l'égalité Un+1=Vn+(1/2Un), montrer que (Wn) est arithmétique de raison r=2
Alors j'ai commencé comme ceci:
Wn+1= Un+1/Vn+1
=> (Vn+(1/2Un))/Vn+1
=> (Vn+(1/2Un))/(1/2Vn)
Après j'ai essayé de remplacer Vn par Un+1-(1/2Un)ce qui m'a donné
(Un+1-(1/2Un)+(1/2Un))/(1/2)*(Un+1-(1/2)Un)
=> Un+1/(1/2)*(Un+1-(1/2)Un)
Et là je bloque .. Je ne sais plus comment faire..
C'est
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
