Exercice sur la recurrence
20 messages
- Page 1 sur 1
Exercice sur la recurrence
Bonjour , je ne comprend pas cet exercice sur les suites.
On considere la suite [Un] definie par u0=0 et pour tout n Un+1=;)12+Un[la racine va jusqu'a Un]
1] Montrer par recurrence que pour tout n , Un<4
2] Montrer que , pour tout n, on a 4-Un+1 < ou egal= 1/4[4-Un] , en deduire que Un converge et calculer sa limite.
Je n'y arrive pas car la demonstration par recurrence est inhabituel et la deuxieme question decoule de la premiere.
On considere la suite [Un] definie par u0=0 et pour tout n Un+1=;)12+Un[la racine va jusqu'a Un]
1] Montrer par recurrence que pour tout n , Un<4
2] Montrer que , pour tout n, on a 4-Un+1 < ou egal= 1/4[4-Un] , en deduire que Un converge et calculer sa limite.
Je n'y arrive pas car la demonstration par recurrence est inhabituel et la deuxieme question decoule de la premiere.
Si on montre pas en premier lieu que les termes de la suite sont positifs (par recurrence, et non pas par observation car ceci n'existe pas en maths n'est ce pas Imod, le fait que U_(n+1) est une racine ne justifie pas la positivité des termes de la suite car cela dépend LARGEMENT de la valeur du premier terme si U0 était égal à -5 je suis désolé la suite n'est pas à termes positifs)
Je repète, si on montre pas (par recurrence) que Un est positif alors le raisonnement par recurrence pour justifier que Un<4 est complètement faux.
REMARQUE : Je parle pas d'existence ici, prouver que les termes sont positifs ne justifie pas l'existence de cette suite récurrente. L'existence se fera par deux étapes, la fonction génératrice et la stabilité par f de l'intervalle choisi.
Je repète, si on montre pas (par recurrence) que Un est positif alors le raisonnement par recurrence pour justifier que Un<4 est complètement faux.
REMARQUE : Je parle pas d'existence ici, prouver que les termes sont positifs ne justifie pas l'existence de cette suite récurrente. L'existence se fera par deux étapes, la fonction génératrice et la stabilité par f de l'intervalle choisi.
Imod a écrit:Je ne comprends pas ton problème sitous les temes ne sont pas positifs mais ils sont tous inférieurs à 4 :doh:
Imod
1/ U_(n+1) est une racine ne justifie pas que la suite est positive.
2/ Faites un raisonnement par récurence pour Un inférieur à 4, vous êtes mieux placé que moi pour découvrir que la question est fausse, vous serez bloqué à l'héridité.
Sur ce coup, je suis plutôt d'accord avec xyz1975 : il est bon de vérifier que la suite existe réellement (ne pas oublier qu'on est au lycée ici...) Pour cela, on peut faire une (seule) récurrence pour  prouvant simultanément
prouvant simultanément  , et tout le monde est content.
, et tout le monde est content.
Et si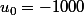 , tous les termes...
, tous les termes...
Imod a écrit:Je ne comprends pas ton problème sitous les temes ne sont pas positifs mais ils sont tous inférieurs à 4 :doh:
Imod
Et si
magnolia86 a écrit:Sur ce coup, je suis plutôt d'accord avec xyz1975 : il est bon de vérifier que la suite existe réellement (ne pas oublier qu'on est au lycée ici...) Pour cela, on peut faire une (seule) récurrence pourprouvant simultanément
, et tout le monde est content.
Et si, tous les termes...
Je ne vais pas polémiquer plus longtemps ( il suffit de relire mes messages ) . Si
Imod
Comme tout a été dit (en sens divers) sur la partie 1, je propose ceci :
Si 0 <= U(n) < 4, on a:
0+12 <= U(n) + 12 < 4+12
12 <= U(n) + 12 < 16
V12 <= V(U(n) + 12) < V16
V12 <= U(n+1) < 4
et a fortiori :
0 <= U(n+1) < 4 (1)
Comme U(0) = 0, par (1), on déduit que U(n) existe et est < 4 pour tout n de N
Rien n'empèche de partir de "Si -12 <= U(n) < 4 ...", mais dans le cas présent ce n'est pas nécessaire.
:zen:
Si 0 <= U(n) < 4, on a:
0+12 <= U(n) + 12 < 4+12
12 <= U(n) + 12 < 16
V12 <= V(U(n) + 12) < V16
V12 <= U(n+1) < 4
et a fortiori :
0 <= U(n+1) < 4 (1)
Comme U(0) = 0, par (1), on déduit que U(n) existe et est < 4 pour tout n de N
Rien n'empèche de partir de "Si -12 <= U(n) < 4 ...", mais dans le cas présent ce n'est pas nécessaire.
:zen:
Black Jack a écrit:Bien sûr que si.
D'ailleur elle est issue de 12 <= U(n) + 12 < 16 qui montre que la quantité qui est sous le radical dans l'expression de U(n+1) est strictement positive.
:zen:
Je préfère arrêter ce type de discussions.....
xyz1975 a écrit:est à termes positifs cela veut dire que les termes sont dans l'intervalle [0;+infini[, encore une fois cela ne justifie pas son existence, lisez le cours sur les suites récurrentes.
heu...
On a bien "
La récurrence montre simultanément l'existence de tous les termes, et un intervalle auquel ils appartiennent.
xyz1975 a écrit:Je préfère arrêter ce type de discussions.....
je comprends.
20 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
