Espace de Hilbert

[anna]

bonjour
soit H espace de hilbert et M fermé de H
la question c'est de montrer que si si M fermé alors M =
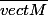
on a M
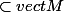
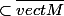
mais je n'arrive pas a montrer que

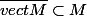
[Archytas]

Qu'appelles tu vectM ? Le sous espace vectoriel engendré par M ? Si M n'est pas lui même un espace vectoriel je pense que ta formule est fausse, essaie de voir ce qui se passe pour M un point de H.

[anna]

bonjour
M est un sous espace vectoriel fermé de H