Fonction holomorphe

[anna]

bonsoir
J'ai besoin de votre aide s'il vous plait a propos d'un exercices
soit f fonction holomorphe sur un ouvert A
montrer que si { z appartient a A / f(z)=0} est d’intérieur non vide alors f est identiquement nulle sur A
et merci

[Robot]

Tu as oublié une hypothèse : l'ouvert doit être connexe.

Cette remarque devrait te mettre sur la voie : il s'agit de montrer qu'un certain ensemble est non vide, ouvert et fermé dans . Par exemple, l'ensemble des où et toutes ses dérivées s'annulent.

[anna]

bonjour
merçi pour votre aide
on pose B= {z / f(z)=0} on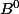 #0 soit ∈
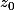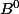
donc ∃ r >0 tel que D (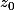 ,r)⊂B or B fermé et ouvert dans un connexe donc B =A
f identiquement nulle sur disque implique de f identiquement nulle sur A

[Robot]

Je ne comprends pas tes affirmations (et ce n'est d'ailleurs pas très lisible, il y a des cafouillis). Où montres-tu que est ouvert ?