Bonjour
j'aurais besoin de vous pour que vous m'expliquez comment on fait pour déterminer 3 constantes telles ques
(x²+x-4)/[(x-2)(x-1)²] = a/(x-2) + b/(x-1) + c/(x-1)²
s'il vous plait, merci
Determiner a b et c
10 messages
- Page 1 sur 1
Re: determiner a b et c
Méthode brutale : on réduit au même dénominateur à droite et on identifie les numérateurs.
Il y a mieux. Regarde n'importe quel cours sur la décomposition en éléments simples.
Il y a mieux. Regarde n'importe quel cours sur la décomposition en éléments simples.
Re: determiner a b et c
Robot a écrit:Méthode brutale : on réduit au même dénominateur à droite et on identifie les numérateurs.
Il y a mieux. Regarde n'importe quel cours sur la décomposition en éléments simples.
Apres avoir reduit au meme denominateur comment identifie t'on les numerateurs?
Re: determiner a b et c
salut
1/ deux fractions de même dénominateur sont égales si et seulement si leur numérateur sont égaux.
2/ deux polynômes sont égaux si et seulement si leur monome de même degré sont égaux.
1/ deux fractions de même dénominateur sont égales si et seulement si leur numérateur sont égaux.
2/ deux polynômes sont égaux si et seulement si leur monome de même degré sont égaux.
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: determiner a b et c
Bonjour;
Je vois que cette journée vous la consacrez aux Mathématiques. Bon courage.
On a^2} = \frac{a}{x-2} + \frac{b(x-1)}{(x-1)^2} + \frac{c}{(x-1)^2} = \frac{a}{x-2} + \frac{b(x-1) + c}{(x-1)^2})
(x-2)+c(x-2)+a(x-1)^2}{(x-1)^2(x-1)} = \frac{(a+b)x^2-(2a+3b-c)x+(a+2b-2c) }{(x-1)^2(x-1)}) ,
,
ceci doit être égal à^2(x-1)}) , donc
, donc 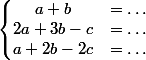 ,
,
ceci vous permettra de trouver a,b et c .
Ceci est une manière de faire: il existe d'autres méthodes plus élégantes qu'on abordera à la fin si vous avez un peu de temps.
Je vois que cette journée vous la consacrez aux Mathématiques. Bon courage.
On a
ceci doit être égal à
ceci vous permettra de trouver a,b et c .
Ceci est une manière de faire: il existe d'autres méthodes plus élégantes qu'on abordera à la fin si vous avez un peu de temps.
Re: determiner a b et c
Vaut mieux que tu connaisses la méthode la plus rapide si tu envisages de passer les concours.
T'as ton expression : (x²+x-4)/[(x-2)(x-1)²] = a/(x-2) + b/(x-1) + c/(x-1)²
Tu peux multiplier à gauche et à droite par (x-1)² puis tu calcules en x=1. A droite il reste plus que "c" et à gauche un nombre.
Tu fais pareil avec (x-2) ça te donne "a". Une fois que tu as a et b tu peux calculer ton expression en un x que tu veux (assez simple de préférence) comme 0 et tu as b.
Pour b tu peux aussi multiplier par (x-1) puis passer à la limite x -> infini (tu peux pas calculer en 1 comme pour les autres à cause du fait que tu tues pas tous les x-1 au dénominateur)
Quand t'auras fait 2/3 fois cette méthode tu trouveras a,b,c en quelques secondes ce qui est un vrai gain de temps sur ceux qui feront la méthode d'identification
T'as ton expression : (x²+x-4)/[(x-2)(x-1)²] = a/(x-2) + b/(x-1) + c/(x-1)²
Tu peux multiplier à gauche et à droite par (x-1)² puis tu calcules en x=1. A droite il reste plus que "c" et à gauche un nombre.
Tu fais pareil avec (x-2) ça te donne "a". Une fois que tu as a et b tu peux calculer ton expression en un x que tu veux (assez simple de préférence) comme 0 et tu as b.
Pour b tu peux aussi multiplier par (x-1) puis passer à la limite x -> infini (tu peux pas calculer en 1 comme pour les autres à cause du fait que tu tues pas tous les x-1 au dénominateur)
Quand t'auras fait 2/3 fois cette méthode tu trouveras a,b,c en quelques secondes ce qui est un vrai gain de temps sur ceux qui feront la méthode d'identification
Re: determiner a b et c
Archytas a écrit:Vaut mieux que tu connaisses la méthode la plus rapide si tu envisages de passer les concours.
T'as ton expression : (x²+x-4)/[(x-2)(x-1)²] = a/(x-2) + b/(x-1) + c/(x-1)²
Tu peux multiplier à gauche et à droite par (x-1)² puis tu calcules en x=1. A droite il reste plus que "c" et à gauche un nombre.
Tu fais pareil avec (x-2) ça te donne "a". Une fois que tu as a et b tu peux calculer ton expression en un x que tu veux (assez simple de préférence) comme 0 et tu as b.
Pour b tu peux aussi multiplier par (x-1) puis passer à la limite x -> infini (tu peux pas calculer en 1 comme pour les autres à cause du fait que tu tues pas tous les x-1 au dénominateur)
Quand t'auras fait 2/3 fois cette méthode tu trouveras a,b,c en quelques secondes ce qui est un vrai gain de temps sur ceux qui feront la méthode d'identification
merci beaucoup pour votre explication
Re: determiner a b et c
aymanemaysae a écrit:Bonjour;
Je vois que cette journée vous la consacrez aux Mathématiques. Bon courage.
On a,
ceci doit être égal à, donc
,
ceci vous permettra de trouver a,b et c .
Ceci est une manière de faire: il existe d'autres méthodes plus élégantes qu'on abordera à la fin si vous avez un peu de temps.
Effectivement , ce fut la journée des maths merci pour votre explication et vos encouragements
Re: determiner a b et c
zygomatique a écrit:salut
1/ deux fractions de même dénominateur sont égales si et seulement si leur numérateur sont égaux.
2/ deux polynômes sont égaux si et seulement si leur monome de même degré sont égaux.
Merci à vous
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
