Equation differentielle

[Simpi]

Bonsoir,
une etude sur le nombre d'oiseaux vivants sur la petite ile d'Hirundo a conduit a stipuler que ce nombre,
t années apres le 21 mars 2016 est solution de l' equation differentielle :
y' = 3sin(2pi*t )y +2000sin(2pi*t)

sachant que la population d'oiseau est de 500 le 21 mars ; determiner le nombre d'oiseaux sur l'ile le 21avril,
le 21 aout.
mes elements de reponses:
d'abord j'ai resolu l'equation differentielle et la solution generale a donné:
y = -2000/3 + k*e^{-3/2pi cos(2pit)}.
pour la determination de k, on 500 oiseaux le 21mars c'est à dire t=0 on a,
500 = -2000/3 +k*e^{-3/2pi} ce qui donne k = 3500/3*e^{3/2pi}.
pour la determination du nombre d'oiseaux le 21 Avril on a t = 1/12 et quand je remplace je trouve
y = 577.
pour le 21 Aout on a t = 5/12 et y = 2177 et c'est là mon probleme. est ce possible d'avoir ce chiffre?

[tim92]

Salut,

On ne voit pas comment tu es arrivé à ta solution générale.
T'as une équation du première ordre de la forme y'+a(t)*y = b(t)
Résolution de l'équation homogène y'+a(t)*y = 0
y'-3*sin(2*pi*t)*y =0
y'/y=3*sin(2*pi*t)
ln(y) = (-3/(2*pi))*cos(2*pi*t) + C
y = K*exp((-3/(2*pi))*cos(2*pi*t))

Pour terminer la résolution de l'équation y'+a(t)*y = b(t) il faut trouver une solution particulière.
Je ne vois pas de solution évidente, et a(t) n'est pas constant.
On utilisera la méthode de variation de la constante:
y = K(t)*exp((-3/(2*pi))*cos(2*pi*t))

y' = K'(t)*exp((-3/(2*pi))*cos(2*pi*t)) +3*K(t)*sin(2*pi*t)*exp((-3/(2*pi))*cos(2*pi*t))

On remplace tous ça dans l'équation y' - 3sin(2pi*t )y = 2000sin(2pi*t)
Ce qui fait K'(t)*exp((-3/(2*pi))*cos(2*pi*t)) = 2000*sin(2pi*t)
K'(t) = 2000*sin(2*pi*t)*exp((3/(2*pi))*cos(2*pi*t))
...
Et pour finir faudra utiliser la condition initial pour trouvé K(t)

[Ben314]

Salut,

mes elements de reponses:
d'abord j'ai resolu l'equation differentielle et la solution generale a donné:
y = -2000/3 + k*e^{-3/2pi cos(2pit)}.
pour la determination de k, on 500 oiseaux le 21mars c'est à dire t=0 on a,
500 = -2000/3 +k*e^{-3/2pi} ce qui donne k = 3500/3*e^{3/2pi}.
pour la determination du nombre d'oiseaux le 21 Avril on a t = 1/12 et quand je remplace je trouve
y = 577.
pour le 21 Aout on a t = 5/12 et y = 2177 et c'est là mon probleme. est ce possible d'avoir ce chiffre?

Oui, je trouve bien exactement la même chose que toi.
Quand à savoir si c'est "raisonnable ou pas", ben il faudrait savoir d'où sort l'équation différentielle [c'est à dire quelle analyse de la situation des population sur l'île à conduit à cette équation] pour savoir si le résultat qu'elle donne est plus ou moins valable.

[aymanemaysae]

J'ai suivi à la lettre la méthode exposée par M. tim92 et j'ai trouvé comme vous :

.

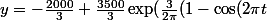Les résultats que vous avez trouvés, je les ai retrouvés et ils me paraissent plausibles, surtout si on considère les nouveaux-nés et les oiseaux migrateurs qui arrivent sur l'île dés le début du printemps.

Edit: Je m'excuse, je n'avais pas vu le message de M. Ben314.

[zygomatique]

salut

Pour terminer la résolution de l'équation y'+a(t)*y = b(t) il faut trouver une solution particulière.
Je ne vois pas de solution évidente, et a(t) n'est pas constant.

l'écriture y' = sin(2pit)[3y + 2000] permet de voir une solution évidente constante ....