Olympiade Divisibilité
Olympiades mathématiques, énigmes et défis
 par Rednakss2508 » 18 Mai 2016, 17:42
par Rednakss2508 » 18 Mai 2016, 17:42
Bonjour, est ce que quelqu'un pourrait m'aider ?
Montrez que si

divise

alors

est divisible par

.
Et aussi
Trouvez les entiers
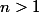
pour lesquels la somme
^{2}+n^{2})
est une puissance d'un nombre premier.
Merci
Modifié en dernier par
Rednakss2508 le 18 Mai 2016, 19:51, modifié 1 fois.

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 18 Mai 2016, 19:33
par Lostounet » 18 Mai 2016, 19:33
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 18 Mai 2016, 20:53
par capitaine nuggets » 18 Mai 2016, 20:53
Salut !
Pour le premier :
Peut-être que ça peut servir :
 = (2-(-1)) ( 2^{n-1} -2^{n-2} +... +2 (-1)^{n-2} +(-1)^{n-1}))
.
Pour le second :
Je ne sais pas si c'est utile, mais
^2+n^2 = \frac{n(n+1)(2n+1)} 6)
.

 par Rednakss2508 » 18 Mai 2016, 21:42
par Rednakss2508 » 18 Mai 2016, 21:42
Oui alors voilà ce que j'ai trouvé pour le premier :

je sais pas si ça peut servir
sinon pour le deuxième j'ai plus :
La somme est égale à
(2n+1)-6}{6} = \frac{(n-1)(2n^{2}+5n+6)}{6})
et on a
;(2n^{2}+5n+6))=pgcd((n-1);13))

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 18 Mai 2016, 22:13
par capitaine nuggets » 18 Mai 2016, 22:13
Rednakss2508 a écrit:Oui alors voilà ce que j'ai trouvé pour le premier :

je sais pas si ça peut servir
sinon pour le deuxième j'ai plus :
La somme est égale à
(2n+1)-6}{6} = \frac{(n-1)(2n^{2}+5n+6)}{6})
et on a
;(2n^{2}+5n+6))=pgcd((n-1);13))
C'est faux :
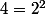
et

.
Ta formule est fausse, je t'ai mis la bonne dans mon précédent message.
Si la tienne était bonne, on aurait pour

,
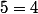
!
 par Rednakss2508 » 18 Mai 2016, 23:38
par Rednakss2508 » 18 Mai 2016, 23:38
capitaine nuggets a écrit: Rednakss2508 a écrit:Oui alors voilà ce que j'ai trouvé pour le premier :

je sais pas si ça peut servir
sinon pour le deuxième j'ai plus :
La somme est égale à
(2n+1)-6}{6} = \frac{(n-1)(2n^{2}+5n+6)}{6})
et on a
;(2n^{2}+5n+6))=pgcd((n-1);13))
C'est faux :
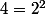
et

.
Ta formule est fausse, je t'ai mis la bonne dans mon précédent message.
Si la tienne était bonne, on aurait pour

,
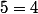
!
n est impair car il divise

donc


(n est impair)

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 13 invités
je sais pas si ça peut servir
je sais pas si ça peut servir
et
.
,
!