Logarithme discret

[matusalem]

Bonjour,

Je vous sollicite pour avoir une piste sur la manière de résoudre ce type d'équation:

2 ^ x = y mod (n)

Je connais n et y et dois donc trouver x.

n n'est pas premier, 2 et n ne sont pas premiers entre eux.
je connais la factorisation de n.

Dans le cas où n est premier avec 2, je connais une méthodologie permettant de calculer x mais pas dans ce cas de figure.

Avez vous une idée de comment on peut procéder?

[L.A.]

Bonjour.

N'as tu pas des précisions supplémentaires ? Parce que cette équation n'a pas de solution en général pour y et n quelconques. Prends par exemple n=4 et y=3. Et même si 2 ne divise pas n, il faut que 2 soit un générateur de (Z/nZ)* ce qui n'est pas toujours vrai.

[matusalem]

Oui hélas tout mon problème vient du fait de l'absence de propriétés fortes entre 2 et n ou seulement sur n (par exemple n premier).

Pour aider voici les valeurs avec lesquelles je travaille:

2 ^ x = 828598094223129383246531684418403172352 mod 3906250000000000000000000000000000000000

Je me demande si un logiciel de type Sage ou Mathematica pourrait résoudre ce genre de problème.

[wserdx]

Les factorisations de y et n sont
[ <2, 38>, <3, 1>, <239, 1>, <4204215211130163183306899, 1> ]
et
[ <2, 34>, <5, 42> ]
Est-ce qu'il s'agit de valeurs particulières ou bien quelconques?

[Doraki]

x doit être au moins 34, donc pose x = 34+y et divise tout par 2^34,
il reste 2^y = truc mod 5^42.

Là, on peut déterminer y de proche en proche :
(Z/5^nZ)* est isomorphe à Z/(4.5^(n-1))Z.
d'abord tu cherches y mod 4 tel que 2^y = truc mod 5,
puis tu cherches y mod 20 tel que 2^y = truc mod 5²
puis tu cherches y mod 100 tel que 2^y = truc mod 5^3 etc

[matusalem]

Merci, effectivement en divisant chaque partie par 2^34, on se retrouve avec 2 et (3906250000000000000000000000000000000000 / 2^34) premiers entre eux.

On résoud ensuite 2^x = (828598094223129383246531684418403172352 / 2^34) mod (3906250000000000000000000000000000000000 / 2^34) avec un algorithme de type "Index calculus" et on peut trouver la solution.

Le résultat final est la solution de cette équation + 34.

[Priz27]

Système d'équation logarithmique;
1/logx+1/logy=7/3. (1)
Log(xy)=log(10^7/2). (2)


Pourriez-vous m'aider svp
Je suis bloqué :cry:

[cauchy-schwartz]

Salut,

C'est mon premier post sur ce forum donc j'espère que vous serez indulgent avec moi

Je suis face à un problème du logarithme discret du même type que proposé ici. Dans ce fil, on propose deux solutions.

Ici, la première:

x doit être au moins 34, donc pose x = 34+y et divise tout par 2^34,
il reste 2^y = truc mod 5^42.

Là, on peut déterminer y de proche en proche :
(Z/5^nZ)* est isomorphe à Z/(4.5^(n-1))Z.
d'abord tu cherches y mod 4 tel que 2^y = truc mod 5,
puis tu cherches y mod 20 tel que 2^y = truc mod 5²
puis tu cherches y mod 100 tel que 2^y = truc mod 5^3 etc

J'ai compris le pourquoi des modulo issu du calcul de l'indicatrice d'Euler. Je souhaitais utiliser le théorème des restes chinois mais 5, 5^2, 5^3,... ne sont pas premier entre eux. Je ne vois donc pas comment résoudre de "proche en proche". Si ce point pouvait être détaillé car il m'échappe complètement....

Merci, effectivement en divisant chaque partie par 2^34, on se retrouve avec 2 et (3906250000000000000000000000000000000000 / 2^34) premiers entre eux.

On résoud ensuite 2^x = (828598094223129383246531684418403172352 / 2^34) mod (3906250000000000000000000000000000000000 / 2^34) avec un algorithme de type "Index calculus" et on peut trouver la solution.

Le résultat final est la solution de cette équation + 34.

De ce second point, je souhaitais utiliser pohlig-hellman en décomposant le modulo en nombres premiers et en utilisant le théorème des restes chinois. Ici mon modulo est 5^k; apparemment, on peut utiliser pohlig-hellman mais j'ai toujours le même blocage quant au fait d'avoir des nombres premiers. J'ai lu textuellement que l'on pouvait utiliser pohlig-hellman pour un modulo égal à une puissance d'un nombre premier mais je n'ai pas trouvé d'exemple concret. Si la méthode pouvait m'être exposée ou me donner des références avec des exemples car toutes mes recherches conduisent à une résolution avec un modulo premier jusqu'à Antoine Joux.

Je sens donc que quelquechose m'échappe dans ce problème et sa résolution que je crois simple.

Voici mon problème: trouver n le plus petit tel que
2^n == R (5^k) où k=42 et R=51293011784756359055849979534

Je vous remercie par avance

CS

[aymanemaysae]

Système d'équation logarithmique;
1/logx+1/logy=7/3. (1)
Log(xy)=log(10^7/2). (2)


Pourriez-vous m'aider svp
Je suis bloqué

Puisque c'est votre premier post, je ne vous dirai pas qu'il faut créer votre propre fil et y éditer votre exercice.

En ce qui concerne votre exercice, je suppose qu'il s'agit d'un système de logarithme décimal (à base 10).



En substituant log(y) par son expression dans la première ligne vous aurez une équation de second degré et par suite les valeurs de log(x) et log(y) ce qui permet d'avoir les valeurs de x et y .

[cauchy-schwartz]

Bonjour,

et merci d'avoir répondu. Mais il y a méprise mon post n'est pas celui de Priz27 mais celui de cauchy-schartz. Mon post est bien dans le thème "logarihtme discret" et non pas le système d'équations sur des logarithmes:

Voici mon problème: trouver n le plus petit tel que
2^n == R (5^k) où k=42 et R=51293011784756359055849979534 (== pour la congruence)

Je demande juste des compléments et du détail sur les méthodes employées.

Merci d'avance.

CS

[Robot]

Si c'est juste la réponse au problème concret, la force brute marche bien : la réponse est 177574654159371801711591377974

[Ben314]

Sinon, il me semble que c'est assez facile de faire un algo. pour ce type de truc :

Déjà un rappel de la théorie bien connue :
Si est premier , et on sait que le groupe multiplicatif des éléments inversible de l'anneau est cyclique et qu'il est engendré par la classe de tout entier tel que :
1) La classe de dans est un générateur du groupe des inversibles de l'anneau .
2) .
Dans ce cas, on a avec et on montre facilement que, pour tout 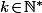on a .

Concernant ton problème consistant à trouver tel que avec connu.
Je pense qu'il faut chercher de proche en proche les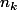 et 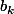tels que (donc )
Pour il y a des tas d'algorithmes pour déterminer 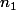et tu en déduit (de plus, si 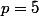, y'a pas vraiment besoin d'algorithme...).
Ensuite, vu que est d'ordre (multiplicatif) dans tu sait que pour un certain (à déterminer). Or


Et il ne te reste plus qu'à évaluer en utilisant le fait que

[cauchy-schwartz]

Merci pour ces précisions d'autant plus que je me suis trompé de R=48230756902085232038896745328
Avant simplification, mon problème originel est le suivant:
trouver n le plus petit tel que:


Je vais regarder la méthode de plus près et la programmer.

Merci bien.

CS

[Robot]

D'où sors-tu tes nombres ? Encore un coup de force brute (plus la remarque stupide que 2^42 divise ton R et qu'il suffit de traiter le problème modulo 5^42) donne la réponse
n = 73522802376970051500945628089
Plutôt que de réinventer l'eau chaude, pourquoi ne pas utiliser des logiciels écrits par des gens compétents ?
En Sage :

[cauchy-schwartz]

Slt,

Je ne dispose pas de SAGE (on peut l'avoir facilement?). Pour ma part, j'en suis resté à MathLab et Mathematica des années 90. Sinon, pour ma propre éducation, je crois que cela peut avoir un intérêt

Merci encore.

CS

[Robot]

Pour SageMath, voir ici.

Ton but n'est pas clair dans ce que tu écris.
Si c'est pour avoir le plaisir d'écrire un programme qui tourne, très bien.
Si c'est pour avoir une réponse rapide (Sage donne la réponse quasi-instantanément) et fiable à un problème spécifique (lequel ? tu ne réponds pas là-dessus), ça ne vaut vraiment pas la peine de se fatiguer.

[cauchy-schwartz]

C'est vrai, je travaille sur un programme qui fait de l'exponentiation modulaire à partir d'une valeur d'entrée qui est l'exposant pour trouver cette valeur R.

Je cherchais donc à résoudre le problème inverse pour obtenir la bonne valeur en entrée. Mes pistes m'ont conduit à chercher si cela était simple théoriquement:

• https://fr.wikipedia.org/wiki/Logarithme_discret
• http://images.math.cnrs.fr/Le-probleme-du-logarithme-discret-en-cryptographie (avec le point sur pohlig-hellman)

Sur ce point Ben314 m'a très bien répondu; en fait, j'ai exposé mon problème parce qu'il me semble (de ce que j'ai lu et compris) que la résolution du cas général est très complexe (modulo premier et très grand) et que je me trouvais dans un cas particulier simple identique au premier post mais que je n'arrivais pas à résoudre par manque de culture mathématique certainement relativement à l'égalité issu du point 2) de Ben314. Je me disais au départ que mon cas pouvait être différent du cas proposé sur le premier post et si je voulais gérer des cas plus généraux, il fallait bien connaître la méthode à appliquer

Mais là où j'ai été très surpris c'est lorsque tu m'as apporté la solution en BF avec SAGE à base de Python car mes tests en PHP ont été ridicules en utilisant les BigInt mais Python gère magnifiquement les grands nombres du moins avec SAGE. C'est donc le langage sur lequel j'aurais dû travailler pour la circonstance. Je vais donc adopter la petite application SAGE à ma panoplie. Cela me permettra de vérfier les petits codes que je produis

J'espère avoir répondu à tes interrogations somme toute justifiées.

CS