Intervalle d'un sous groupe discret
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 03 Juil 2006, 01:11
par nuage » 03 Juil 2006, 01:11
Salut,
ça me semble bien, mais pourquoi une division ?
Il me semble que
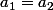
suffit.
Une remarque : compte tenue des hypothèses ajoutées l'intervalle est

tout entier. Qu'en est-il si l'ordre n'est pas total ?
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 03 Juil 2006, 01:11
par tize » 03 Juil 2006, 01:11
Je pense qu'avec une construction assez simple on peut prouver l'existence...
Si

est le plus petit élément de
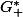
, on doit pourvoir considerer
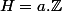
comme un intervalle qui est aussi un sous groupe de

. En effet si
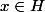
et
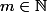
avec
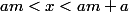
et comme l'ordre est total et

est un groupe :
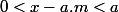
avec
\in G_{+}^{*})
ce qui est absurde par définition de

. Donc

est un intervalle.
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 03 Juil 2006, 01:14
par tize » 03 Juil 2006, 01:14
nuage a écrit:Une remarque : compte tenue des hypothèses ajoutées l'intervalle est

tout entier...
Je ne comprends pas ...

lui n'est pas forcement isomorphe à


-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 03 Juil 2006, 01:19
par nuage » 03 Juil 2006, 01:19
Salut,
tize a écrit:Je ne comprends pas ...

lui n'est pas forcement isomorphe à

Regarde la démonstration que tu viens d'écrire : G est discret et totalement ordonné, il a donc un plus petit élément strictement positif etc...
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 03 Juil 2006, 01:26
par tize » 03 Juil 2006, 01:26
ba oui mais que dir alors de
)
avec l'ordre lexicographique... le sous groupe des éléments qui s'écrivent
)
avec
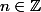
est un intervalle isomorphe à

different de
)
Dans ma demo jutilise le fait que les
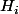
sont isomorphes à
)
ce qui n'est a priori pas le cas de


-
nuage
- Membre Complexe
- Messages: 2214
- Enregistré le: 09 Fév 2006, 22:39
-
 par nuage » 03 Juil 2006, 01:51
par nuage » 03 Juil 2006, 01:51
Salut,
en effet : j'ai fait une grave erreur.
Avec mes excuses;
nuage :
-
mathelot
 par mathelot » 03 Juil 2006, 11:25
par mathelot » 03 Juil 2006, 11:25

étant discret, il existe un voisinage de zéro dans G qui ne contient que zéro.
La topologie venant de l'ordre, il existe
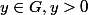
, tel que
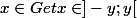
implique

. un tel y ayant cette propriété est unique. Le sous-groupe
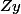
devrait être un intervalle.
Est-ce qu'il faut supposer le groupe non réduit à zéro et la topologie séparée ?
euh, je crois que je suis en retard sur la discussion.
-
tristan
- Membre Relatif
- Messages: 113
- Enregistré le: 01 Mai 2005, 01:14
-
 par tristan » 03 Juil 2006, 15:03
par tristan » 03 Juil 2006, 15:03
J'aime bien la demonstration d'unicité.
J'avais aussi l'impression que ,vu la construction, on avait
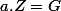
. Mais puisque G n'est pas archimédien on ne peut pas forcément "caser" systématiquement ses elements dans une inégalité du type
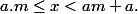
Merci beaucoup
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités