Dénombrement discret qui fait du bruit
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 09 Sep 2006, 11:26
par Flodelarab » 09 Sep 2006, 11:26
Bonjour les universitaires ! :we:
On a donc une matrice de terme générale

de sorte que:
=(1,1) \qquad, \qquad a_{1,1} = 1 \\pour (i,j)\neq (1,1) \qquad,\qquad a_{i,j} = \sum_{k=1}^{i-1}a_{k,j} + \sum_{m=1}^{j-1}a_{i,m} })
Ayant la flemme de calculer la forme générale de

en fonction de i et j, j'ai fait bosser excel.
Il y a donc 470010 façon pour une tour d'arriver à H8 en partant de A1 d'un échiquier classique (8 cases sur 8 cases)
Commet trouver la formule générale en fonction de i et j ?

On ne considérera donc, dorénavant, que les i inférieurs aux j
2^{j-3} \\ pour\qquad j\ge n \qquad,\qquad a_{n,j}= ???) Qui a une idée ? Qui veut participer ?
Qui a une idée ? Qui veut participer ?
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 09 Sep 2006, 13:42
par tize » 09 Sep 2006, 13:42
Bonjour Flordelarab
je me penche sur le problème...
j'ai essayé de trouver la 3ième ligne de la matrice et au début : 2,5,14,37,94...
ca ne m'a pas l'air très evident comme problème (c'est une question que tu t'es posé ou ca vient d'un exercice ?) j'ai essayé sur "The On-Line Encyclopedia of Integer Sequences" ca ne donne rien...
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 09 Sep 2006, 14:01
par Flodelarab » 09 Sep 2006, 14:01
Oh purée!
Tu m'ecris les nombres de la ligne et je me rends compte que j'ai fais une faute.
96 au lieu de 94.
G de nouveau une piste ptet valable.
to be continued
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 09 Sep 2006, 20:09
par Flodelarab » 09 Sep 2006, 20:09
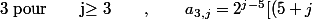(6+j)-16])
ça m'enerve! Tous ce simplifie. Je dois etre sur une formule connue mais je la trouve pas!
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 11 Sep 2006, 09:38
par nox » 11 Sep 2006, 09:38
moi je reste sur mon
})
(moi boulet ? naaaaaaan jamais :we: )
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 11 Sep 2006, 10:56
par Flodelarab » 11 Sep 2006, 10:56
nox a écrit:Pour chaque possibilité on a i mouvement vers le bas et j vers la droite. Il faut donc multiplier par

pour placer les i parmi i+j
donc ca serait
})
hem...t'en dis quoi Flo ?
- Je m'étonne du caractère asymétrique de ta formule
- Je vois pas ce que vient faire le j devant.
- J'applique ta formule et ne trouve pas la bonne reponse (470010)
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 11 Sep 2006, 11:52
par nox » 11 Sep 2006, 11:52
Flodelarab a écrit:- Je m'étonne du caractère asymétrique de ta formule
i et j c'est des variables muettes on s'en cogne ^^
je vois pas pourquoi ca serait symétrique
Flodelarab a écrit:
Je vois pas ce que vient faire le j devant.
c'est expliqué dans le post "petit probleme" sur college :p
Flodelarab a écrit:
J'applique ta formule et ne trouve pas la bonne reponse (470010)
t'as la réponse ?? ba comment ??
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 11 Sep 2006, 12:43
par Flodelarab » 11 Sep 2006, 12:43
nox a écrit:t'as la réponse ?? ba comment ??
Ptet tu as lu en diagonale.
La modélisation est
juste. Le cas particulier est
juste. La formule d'une case en fonction des précédentes est
juste. Mais la formule en fonction d'un i et j quelconque est inconnue. C ça que l'on cherche.
J'aimerais etre capable de calculer ce nombre, si, comme un boulet,
- j'ai amené un damier au lieu d'un echiquier
- j'ai amené un go ban au lieu d'un echiquier
- j'ai amené une grille de morpion au lieu d'un echiquier
- j'ai amené un sudoku au lieu d'un echiquier
- je tombe en panne d'essence en F3
- je tombe en panne d'essence en B6
- etc ...
PS: La symétrie ? Elle est évidente. T'as essayer de remplir l'echiquier avec les nombres comme je le préconisais pour notre collegienne ?
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 11 Sep 2006, 12:45
par nox » 11 Sep 2006, 12:45
ok donc en fait on bosse juste pas sur le même truc.
Moi j'étais sur le nombre de "façons" d'aller de A1 à H8 avec une tour...donc pas "trajectoire".
Bon ba tout est bien alors...je bouletterai plus ^^
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 11 Sep 2006, 12:53
par Flodelarab » 11 Sep 2006, 12:53
nox a écrit:Moi j'étais sur le nombre de "façons" d'aller de A1 à H8 avec une tour...donc pas "trajectoire".
Mais moi aussi
Le nombre de trajectoire on l'avait deja trouvé.
c'etait

...
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 11 Sep 2006, 12:54
par nox » 11 Sep 2006, 12:54
mais alors ton truc avec le triangle de pascal marche pu par exemple dans le cas de la panne d'essence non ?
donc le numérique que tu sors est plus valable !!
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 11 Sep 2006, 12:55
par Flodelarab » 11 Sep 2006, 12:55
J'avais proposé un triangle de pascal "adapté" dont je n'ai pas la formule.
Je peux te dire par exemple qu'il y a 5 façon d'aller en C2 ....
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 11 Sep 2006, 12:56
par nox » 11 Sep 2006, 12:56
ok donc si t'as pas la formule comment t'as sorti le numérique ?
EDIT : ok c'est bon j'ai appris à lire entre temps
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 11 Sep 2006, 12:57
par Flodelarab » 11 Sep 2006, 12:57
Par un bout de papier et de l'huile de coude.
Je calcule pour chaque case le nombre de façon d'y aller.
c la somme de toutes les precedentes sur la ligne et colonne.
Formule citée en haut de cette page
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 11 Sep 2006, 12:59
par nox » 11 Sep 2006, 12:59
wai j'ai édité entre temps ^^
PS : jm'étais planté dans la formule, j'imagine que c'est toujours faux...mais bon...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
