Svp, Montrer que ,E={l'espace vectoriel des suites complexes (an)n telles que [Sum de n=0 à +00 (module²(an))]<+00}
muni du produit scalaire E²-->C, ((an)n,(bn)n)---> sum de n=0 à +00 [an.bar(bn)], est un espace de Hilbert complexe.
Rappel= un espace prehilbertien complet est appelé un espace de Hilbert.
J'éspère que toutes les notations sont claires, et merci d'avance pour votre indications.
Espace Hilbert
9 messages
- Page 1 sur 1
Re: Espace Hilbert
On te dit dans l'énoncé que c'est un produit scalaire. On peut donc supposer qu'il n'y a pas besoin de le démontrer (en tout cas, ce n'est pas dur).
Reste la complétude. Qu'est-ce que ça veut dire ? Que faut-il montrer ?
Reste la complétude. Qu'est-ce que ça veut dire ? Que faut-il montrer ?
Re: Espace Hilbert
Précisement:On dit que A est complet si toute suite de Cauchy à élements dans A converge dans A.
Re: Espace Hilbert
Eh bien tu te donnes une suite de Cauchy d'éléments de E, et tu montres qu'elle a une limite dans E. La démarche est claire, n'est-ce pas ?
Quelques étapes pour te guider
Soit_p) une suite de Cauchy d'éléments de
une suite de Cauchy d'éléments de  ; chaque
; chaque 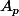 est une suite
est une suite _n) .
.
Exprimer ce que veut dire le fait que_p) est de Cauchy.
est de Cauchy.
Trouver une suite_n) de nombres complexes candidate à âtre la limite (que prendre pour
de nombres complexes candidate à âtre la limite (que prendre pour  ?). Montrer que
?). Montrer que  appartient bien à
appartient bien à  , et établir la convergence de
, et établir la convergence de _p) vers
vers  .
.
Quelques étapes pour te guider
Soit
Exprimer ce que veut dire le fait que
Trouver une suite
Re: Espace Hilbert
Tu n'as vraiment aucune idée sur ce que pourrait être  ?
?
Pourtant, ça s'impose quand on pense à la limite de la suite des suites_n) quand
quand  tend vers l'infini !
tend vers l'infini !
Pourtant, ça s'impose quand on pense à la limite de la suite des suites
Re: Espace Hilbert
Je suis vraiment étonné que tu n'arrives pas à te dire que si on veut que la limite des suites _n) pour
pour  tendant vers l'infini soit égale à la suite
tendant vers l'infini soit égale à la suite _n) , il paraît naturel d'essayer
, il paraît naturel d'essayer  . Que pourrait-on faire d'autre ?
. Que pourrait-on faire d'autre ?
Une fois que le bon sens nous a amené à ça, on n'a pas fini.
Il reste:
- à s'assurer que est bien définie pour tout
est bien définie pour tout  , autrement dit que la suite
, autrement dit que la suite _p) converge;
converge;
- à vérifier que la suite_n) est bien un élément de
est bien un élément de  ;
;
- à montrer que la suite_p) converge bien vers
converge bien vers  dans
dans  .
.
Une fois que le bon sens nous a amené à ça, on n'a pas fini.
Il reste:
- à s'assurer que
- à vérifier que la suite
- à montrer que la suite
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
