Bonjour a tous ,
J'essaye de faire un exercice de maths sur les propriétés de l'intégrale mais j'epprouve quelques difficultes a factoriser une fonction
Un+1-Un = primitive (1-0) ((1-x)^n+1*e^-3x -[(1-x)^n*e-3x)] voila j'espère une réponse pour pouvoir continuer l'exercice ! Merci
Propriété de l'intégrale
9 messages
- Page 1 sur 1
Salut,
Déjà, j'arrive pas à lire l'énoncé : met toi au MimeTeX
Ton truc, c'est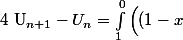^n+1\times e^{-3x}-(1-x)^ne^{-3x}\Big)dx\) ?
?
Si c'est ça, il manque pas mal de parenthèses ( par exemple e^(-3x) ), les crochets ( [(1-x)^n*e-3x)] ) servent à rien, c'est pas "la primitive(1-0)" mais "l'intégrale de 1 à 0" et enfin il manque le à la fin.
à la fin.
quentin59000 a écrit:Un+1-Un = primitive (1-0) ((1-x)^n+1*e^-3x -[(1-x)^n*e-3x)]
Déjà, j'arrive pas à lire l'énoncé : met toi au MimeTeX
Ton truc, c'est
Si c'est ça, il manque pas mal de parenthèses ( par exemple e^(-3x) ), les crochets ( [(1-x)^n*e-3x)] ) servent à rien, c'est pas "la primitive(1-0)" mais "l'intégrale de 1 à 0" et enfin il manque le
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
bonjour
tout d'abord quelle est exactement la fonction?
pourrais tu la re-ecrire correctement avec parentheses et crochets?
en effet le resultat que tu affiches semble bizarre .....
J'ai trouvé un+1 -Un = [(1-x)-1) (1-x)^n e (-3x)]
a/ (1-x)-1 = -x
b/ dans l'integrale bornée il ne doit plus y avoir de x !!!!!!!!
ajout: je pense que Zygomatique a raison, mais ............il faut deviner!
tout d'abord quelle est exactement la fonction?
pourrais tu la re-ecrire correctement avec parentheses et crochets?
en effet le resultat que tu affiches semble bizarre .....
J'ai trouvé un+1 -Un = [(1-x)-1) (1-x)^n e (-3x)]
a/ (1-x)-1 = -x
b/ dans l'integrale bornée il ne doit plus y avoir de x !!!!!!!!
ajout: je pense que Zygomatique a raison, mais ............il faut deviner!
Merci pour vos réponses . Veuillez m'excuser j'ai du mal à écrire en langage mathématiques sur informatique.
La question est la suivante :
Établir pour tout entier n de N , l'inégalité suivante Un+1-Un < 0.
Sachant que Un = /int_0^1 (1-x)^n e^{-3x}dx
J'ai donc posé l'inéquation en remplaçant n par n+1 pour obtenir Un+1
ensuite j'utilise la propriété de linéarité de l'intégrale pour obtenir une intégrale monobloc mais c'est après dans la factorisation que j'ai du mal , pourtant j'arrive à trouver que Un+1 -Un est bien <0 pourriez vous m'aider ?
La question est la suivante :
Établir pour tout entier n de N , l'inégalité suivante Un+1-Un < 0.
Sachant que Un = /int_0^1 (1-x)^n e^{-3x}dx
J'ai donc posé l'inéquation en remplaçant n par n+1 pour obtenir Un+1
ensuite j'utilise la propriété de linéarité de l'intégrale pour obtenir une intégrale monobloc mais c'est après dans la factorisation que j'ai du mal , pourtant j'arrive à trouver que Un+1 -Un est bien <0 pourriez vous m'aider ?
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
