Démonstration analyse

[quenouille]

Bonsoir (ou bonjour?)
Je suis bloqué depuis ce matin (hier matin) sur une démonstration.
Il faut que je démontre que si la limite en +infini de f' est 0 alors f(dérivable sur tout R) converge vers une limite L.

Quelqu'un aurait-il une piste?

[MouLou]

?

Es tu sur de ton énoncé?

[quenouille]

Certain, c'est une question de mon DM de math.
On sait que f est dérivable sur R et que la limite en l'infini de sa dérivé est 0.
Et il faut démontrer que la fonction converge en l'infini.

C'est simple à visualiser et ça parait logique parce que si la dérivé en l'infini tend vers 0, ça veut dire qu'en l'infini, l'image de la fonction ne varie quasiment plus et donc que f converge.
Mais si je dis ça dans mon dm j'ai 0 ....

[MouLou]

Mais c'est surtout faux! regarde .

En fait, oui, la dérivée tend vers 0, mais tendre vers 0 ne veut pas dire etre nulle. la fonction racine augmente très lentement, de plus en plus lentement, mais ca ne l'empeche pas d'aller aussi haut qu'elle le veut, un vrai exemple de persevérance

[ilikoko123]

Moulou c'est peut car ta fonction n'est pas dérivable sur R

[quenouille]

racine de x comme ln ne sont pas dérivables sur R

[MouLou]

On s'en fout de ca a vrai dire, ce qui compte c'est le comportement en l'infini. Si tu preferes on peut imaginer la fonction racine sur 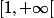, et une autre fonction quelcquonque sur 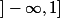avec raccordement C^{1}. La fonction en + l'infini ca reste la fonction racine, dont la dérivée tend vers 0 mais qui tend vers

[quenouille]

Tu as l'air d'avoir raison mais t'es sur que f sera dérivable sur 1 ? C'est quoi un raccordement C^1 ?
Peut-être que le fait que l'énoncé exige que f soit dérivable sur R restreint nos possibilités et qu'on ne puisse (par exemple) que utiliser des fonctions élémentaires.

[MouLou]

Bah c'est toujours possible, y'en a forcément un qui existe, suffit qu'elle ait la même dérivée. Tiens jvais prendre f(x)=x sur ]-oo,1], et f(x)=sqrt(x) sur [1,+oo[, f(1)=1, f'(1)=1 a gauche et a droite, donc jai mon raccordement C^1, (mais pas C^2)

Edit: Pardon je n'avais pas vu ta question sur le raccordement C1. Un raccordement quand tu mets bout a bout des fonctions, disons 2. Par exemple dans mon cas je prends 2 fonctions et je veux les raccorder en 1.

Le soucis évidement et qu'elles ont beau etre aussi régulières que tu veux, par exemple , si je les mets bout a bout, j'obtiens pas forcément une fonction régulière, (c'est même pas forcément continue). Quand je dis raccordement C^1, je veux dire que quand je fais cette opération, j'obtiens toujours une application C^1. La condition est que au point de raccordement, les 2 fonctions et leurs dérivées aient la même valeur, ce qui est le cas avec 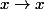et la fonction racine quand je les raccorde au point 1.

[quenouille]

Ca marche. Mais dans ton exemple, la dérivé de racine de x en 1 c'est 1/2 et ce n'est pas égal à la dérivé de f(x)=x (1)

[MouLou]

Pardon tu as mille fois raison jai oublié le facteur 1/2! alors on va dire x/2 sur ]-oo,1]! :id:

[ilikoko123]

cette fonction n'est même pas continue :(

[quenouille]

haha! Bah j'irais dire ça la semaine prochaine à mon prof de math pendant ses heures de réception ^^
Mais ça me parait bizarre parce que si c'était pas faisable, le prof nous aurait déjà envoyé un mail pour nous prévenir... (Le dm est à rendre pour lundi soir....)

[MouLou]

Oui lol je perds la continuité à présent, je suis fatigué. prenons x/2+1/2! :mur:

[quenouille]

cette fonction n'est même pas continue

Oui mais à la place de x/2 on peut utiliser x/2+1/2

[Ben314]

Sinon, ne t'emmerde pas : tu prend ou bien qui sont clairement C^infini sur R tout entier, dont les dérivées tendent gentiment vers 0 lorsque x->+oo et les fonction, elle, elle tendent vers +oo

Plus vicieux : tout ce qu'il y a de plus C^infinie sur R tout entier, la dérivée tend vers 0 et pourtant la fonction ne tend vers rien du tout (elle fait des oscillations de plus en plus grandes...)

C'est simple à visualiser et ça parait logique...

Comme quoi, méfie toi de ce qui te semble "simple à visualiser et plutôt logique".... :zen:

[quenouille]

Haha! J'ai l'air c** mais ça me paraissait logique.
Je n'aurais jamais imaginé que l'énoncé de mon dm était faux ^^

[MouLou]

Je pense qu'à première vu c'est "logique" pour tout le monde que f va converger. Et se rappeler de ce genre d'exemple t'évitera souvent de dire des anneries qui parraissaient pourtant logiques tu verras! :D. Mais c'est pas non plus une raison pour partir dans des délires métaphysiques ou tout est mensonge. La plupart du temps ce genre d'intuition sera juste

[Ben314]

ça semble effectivement un peu contre intuitif la première fois qu'on le voit puis... on s'habitue et on fini par trouver ça normal.

C'est quasiment la même chose que si tu as une suite telle que .
On pourrait se dire que les termes sont de plus en plus proche les uns des autres donc que la suite en question a forcément une limite.
Ben non, c'est vrai que pour passer d'un terme au suivant on ajoute un truc quasi nul, mais le problème c'est qu'on le fait une infinité de fois avant "d'arriver à l'infini".
On a donc 0 x +oo et... c'est une forme indéterminée : on peut pas prévoir ce que ça va donner....

Sinon, juste pour voir au niveau intuition ce que tu en pense, la réciproque du truc en question, c'est à dire :
Si une fonction F est dérivable sur R et que F(x) tend vers une limite finie L lorsque x->+oo alors F'(x) tend vers 0 lorsque x->+oo.
Tu en pense quoi ; vrai ou faux ?

[quenouille]

Mon intuition me dit que ç'est vrai parce que pour tout x>M(epsilon) on aura |f(x)-L| Donc plus on augmente M plus on pourra avoir un epsilon petit. (edit: je veux dire que pour n'importe quel epsilon aussi petit qu'il soit, on trouvera un M tel que pour tout x>M |f(x)-L|C'est flippant de se dire que des trucs qui nous paraissent intuitivement évidents sont en fait complètement faux :mur: :mur: