Raisonnement par récurrence
12 messages
- Page 1 sur 1
Raisonnement par récurrence
On considère une suite (Un) telle que pour tout entier naturel n>ou égal à 0, Un+1<ou égal à a*Un, où a est un réel positif. Montrer par récurrence que pour tout entier naturel n, Un<ou égal à a exposant n *Uo
Salut !
Avnt toute chose, ce qu'il faut savoir, c'est qu'un raisonnement par récurrence est composé de deux étapes :
1) Initialisation : on vérifie que pour le premier indice, la propriété est vérifiée ;
2) Hérédité : on montre que si l'on suppose la propriété vraie pour un certain rang k, alors elle est vraie au rang suivant k+1.
Commence déjà par l'initialisation.
:+++:
Avnt toute chose, ce qu'il faut savoir, c'est qu'un raisonnement par récurrence est composé de deux étapes :
1) Initialisation : on vérifie que pour le premier indice, la propriété est vérifiée ;
2) Hérédité : on montre que si l'on suppose la propriété vraie pour un certain rang k, alors elle est vraie au rang suivant k+1.
Commence déjà par l'initialisation.
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Notons  , la propriété :
, la propriété :
[CENTER]"pour tout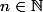 ,
,  ".[/CENTER]
".[/CENTER]
Initialisation : il s'agit de montrer que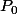 est vraie. Remplace donc tout bêtement
est vraie. Remplace donc tout bêtement  par
par  ; que vaut
; que vaut  ? que vaut
? que vaut  ? Qu'en déduis-tu ?
? Qu'en déduis-tu ?
[CENTER]"pour tout
Initialisation : il s'agit de montrer que
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
