Bonjour, j'ai un problème en maths et mes cours commencent à dater, je me permet donc de poser la question sur ce site.
Le problème est défini sur l'image que j'ai mis en lien :
http://www.cjoint.com/c/EFwjGXf6niG
Je veux calculer l'abscisse x2 du point 2 de telle sorte que A soit égal à 0.35.
Je connais x1,x3,y1,y2,y3.
Par ailleurs la courbe violette est une courbe de Bézier définie par :
x(t) = (1-t)²*x0 + 2t(1-t)*x1 + t²*x2
y(t) = (1-t)²*y0 + 2t(1-t)*y1 + t²*y2
Avec t défini entre 0 et 1.
Avez-vous une idée ?
Aire et courbe paramétrée
15 messages
- Page 1 sur 1
par Ben314 » 22 Juin 2015, 11:17
Salut,
Ton A, c'est l'aire de la surface délimitée par la courbe d'un coté et le segment reliant les 2 points de l'autre ?
Ton A, c'est l'aire de la surface délimitée par la courbe d'un coté et le segment reliant les 2 points de l'autre ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par Ben314 » 22 Juin 2015, 12:57
Salut,
Ton A, c'est l'aire de la surface délimitée par la courbe d'un coté et le segment reliant les 2 points de l'autre ?
Si oui, l'aire vaut les 2/3 de celle du triangle formé par tes 3 points (si je me suis pas gouré dans les calculs, mais ça semble "plausible)
Ton A, c'est l'aire de la surface délimitée par la courbe d'un coté et le segment reliant les 2 points de l'autre ?
Si oui, l'aire vaut les 2/3 de celle du triangle formé par tes 3 points (si je me suis pas gouré dans les calculs, mais ça semble "plausible)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par titou1523 » 22 Juin 2015, 13:14
Salut, merci de ta réponse oui A est bien l'aire formée par le segment d'un côté et ma courbe paramétrée de l'autre.
J'avoue ne pas du tout comprendre pourquoi ça ferait 2/3 de l'aire du triangle formée par les 3 points. Est-ce une propriété des courbes de Bézier ?
J'avoue ne pas du tout comprendre pourquoi ça ferait 2/3 de l'aire du triangle formée par les 3 points. Est-ce une propriété des courbes de Bézier ?
par Ben314 » 22 Juin 2015, 22:49
J'ai pas regardé pour celles avec plus de 3 points si la surface est "facilement" exprimable (elle l'est clairement, mais la formule est-elle "simple" ?)
Pour 3 points, y'a des tas de façon de procéder :
1) Vu que la notion de "courbe de Bézier" est stable par transformation affine (les points sont des barycentres), il suffit de regarder le cas très simple où les extrémités sont A:(0,0), B:(2,0) et où le "point de contrôle" est C:(1,1).
On a alors M(t)=(2t , 2t-2t²))=(x,f(x)) où f(x)=x-x²/2 donc la surface sous la courbe estdx=\frac{2}{3})
alors que la surface du triangle est 1.
Comme les transformation affine ne font que multiplier les surfaces par une constante, dans le cas où A,B,C sont quelconque, la surface entre la courbe et le segment sera tout le temps égale au 2/3 de celle du triangle.
2) Si A et B sont les extrémités et C le point de contrôle, alors la surface dont on cherche l'aire est celle "balayée" par le segment
où 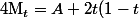\vec{AC}+t^2\vec{AB})
, or une petite variation dt de t donne un petit triangle dont les vecteurs formant deux cotés sont 
et 
dont l'aire est )
(le signe dépendant du fait que les vecteur sont dans le sens direct ou pas)
L'aire totale de la surface balayée est donc :
dt)
\vec{AC}+t^2\vec{AC}\,,\,(2-4t)\vec{AC}+2t\vec{AB}\Big)dt)
 \int_0^1 \big(4t^2(1-t)-t^2(2-4t)\big)dt)
\times\frac{2}{3})
Et l'aire du triangle ABC est)
Pour 3 points, y'a des tas de façon de procéder :
1) Vu que la notion de "courbe de Bézier" est stable par transformation affine (les points sont des barycentres), il suffit de regarder le cas très simple où les extrémités sont A:(0,0), B:(2,0) et où le "point de contrôle" est C:(1,1).
On a alors M(t)=(2t , 2t-2t²))=(x,f(x)) où f(x)=x-x²/2 donc la surface sous la courbe est
Comme les transformation affine ne font que multiplier les surfaces par une constante, dans le cas où A,B,C sont quelconque, la surface entre la courbe et le segment sera tout le temps égale au 2/3 de celle du triangle.
2) Si A et B sont les extrémités et C le point de contrôle, alors la surface dont on cherche l'aire est celle "balayée" par le segment
L'aire totale de la surface balayée est donc :
Et l'aire du triangle ABC est
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par titou1523 » 23 Juin 2015, 10:40
Merci beaucoup de ta réponse, je comprend mieux maintenant.
J'ai cependant une question pour une courbe de Bézier avec plus de points de contrôle, par exemple 2 (je les appelle C et D).
Aura-t-on la même expression de l'aire totale mais avec 
du type ^2\vec{AC}+3t^2(1-t)\vec{AD}+t^3\vec{AB})
?
J'ai cependant une question pour une courbe de Bézier avec plus de points de contrôle, par exemple 2 (je les appelle C et D).
Aura-t-on la même expression de l'aire totale
par Ben314 » 23 Juin 2015, 12:30
Oui, tout à fait.
Et on peut même le faire avec n points, mais je ne sais pas si la formule "finale" se simplifie ou pas...
Et on peut même le faire avec n points, mais je ne sais pas si la formule "finale" se simplifie ou pas...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par titou1523 » 23 Juin 2015, 12:43
Ce qui est étrange c'est que le déterminant est alors une matrice 2*3, sans doute ai-je fait une erreur... Normalement, le déterminant est une matrice carrée
par Lostounet » 23 Juin 2015, 13:22
Je croyais que le déterminant était un nombre...?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
par titou1523 » 23 Juin 2015, 13:37
Lostounet a écrit:Je croyais que le déterminant était un nombre...?
Je me suis mal exprimé, le déterminant est effectivement un nombre mais calculer le déterminant d'une matrice ne se fait que pour des matrices carrées. Ici j'ai 2 vecteurs qui ont chacun 3 coordonnées...
par Ben314 » 24 Juin 2015, 08:13
Tes points sont dans R^3 ?
Les calculs çi dessus correspondent à des points/vecteurs de R^2.
Dans R3, c'est pas clair vu que si les points ne sont pas coplanaires (donc la courbe n'est pas contenue dans un plan), la notion de "surface entre la courbe et le segment" devient plutôt caduque...
Les calculs çi dessus correspondent à des points/vecteurs de R^2.
Dans R3, c'est pas clair vu que si les points ne sont pas coplanaires (donc la courbe n'est pas contenue dans un plan), la notion de "surface entre la courbe et le segment" devient plutôt caduque...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par titou1523 » 25 Juin 2015, 08:46
Mes points sont bien dans R^2 mais avec la nouvelle expression de M(t) qui fait intervenir AC, AB et AD je ne sais pas calculer le déterminant.
par Ben314 » 25 Juin 2015, 14:53
Ton déterminant a "content" effectivement pour ces deux paramètres trois vecteurs, mais ce sont des vecteur de R² et on les ajoute ce qui ne fait qu'un vecteur de R².
Sinon, pour rester "théorique", tu peut aussi développer le déterminant et utiliser son antisymétrie.
Avec 3 points, donc avec, ça donnerais :
^2\vec{AC}+3t^2(1-t)\vec{AD}+t^3\vec{AB}\,,<br />\,3(1-4t+3t^2)\vec{AC}+3(2t-3t^2)\vec{AD}+3t^2\vec{AB}\Big)dt)
 \int_0^1 \big(9t(1-t)^2(2t-3t^2)-9t^2(1-t)(1-4t+3t^2\big)dt)
 \int_0^1 \big(9t^3(1-t)^2-3t^3(1-4t+3t^2\big)dt)
 \int_0^1 \big(9t^4(1-t)-3t^3(2t-3t^2\big)dt)
\times\frac{3}{10}\ <br /> +\ \frac{1}{2}\det(\vec{AC},\vec{AB}\big)\times\frac{3}{10}\ <br /> +\ \frac{1}{2}\det(\vec{AD},\vec{AB}\big)\times\frac{3}{5})
Faire attention qu'il s'agit d'aire algébrique, c'est à dire que, si les points de contrôle B et C sont de part et d'autre de la droite (AB), l'aire calculée çi dessus comptera comme positive la partie de la surface d'un coté de la droite (AB) et négative celle de l'autre coté.
Sinon, pour rester "théorique", tu peut aussi développer le déterminant et utiliser son antisymétrie.
Avec 3 points, donc avec
Faire attention qu'il s'agit d'aire algébrique, c'est à dire que, si les points de contrôle B et C sont de part et d'autre de la droite (AB), l'aire calculée çi dessus comptera comme positive la partie de la surface d'un coté de la droite (AB) et négative celle de l'autre coté.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par Ben314 » 26 Juin 2015, 14:27
Si on cherche à voir ce que donne le cas général Pour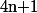 
points de contrôle 
, on a
\vec{AC_k}\)
avec ={n\choose k}t^k(1-t)^{n-k}\)
(polynôme de Bernstein) donc '\!(t)={n\choose k}t^{k-1}(1-t)^{n-k-1}(k-nt)\)
\vec{AC_k}\,,\,\sum_{\ell=1}^{n}(P^n_\ell)'\!(t) \vec{AC_\ell}\Big)dt\ <br />=\ \frac{1}{2}\sum_{1\leq k,\ell\leq n}\Big(\det\big(\vec{AC_k},\vec{AC_\ell}\big)\int_0^1P^n_k(P^n_\ell)'\Big)\ <br />=\ \frac{1}{2}\sum_{1\leq k<\ell\leq n}\lambda_{k,\ell}\det\big(\vec{AC_k},\vec{AC_\ell}\big))
avec, pour tout
,
'-P^n_\ell(P^n_k)'\Big)<br />=\ (\ell-k){n\choose k}{n\choose l} \int_0^1 t^{k+\ell-1}(1-t)^{2n-k-\ell-1}dt\ <br />=\ \frac{(\ell-k){n\choose k}{n\choose l}}{{2n-2\choose k+\ell-1 }} \int_0^1 P^{2n-2}_{k+\ell-1}\ <br />=\ \frac{(\ell-k){n\choose k}{n\choose l}}{(2n-1){2n-2\choose k+\ell-1 }})
Reste à voir si on peut (plus ou moins) interpréter géométriquement le résultat en terme de surface de différents triangles. Il y en a des tas qui apparaissent et la façon de mener les calculs çi dessus en privilégiant l'origine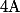
n'est pas la meilleure façon de "voir" ce qu'il se passe (mais les calculs sont simples...)
Je vais regarder avec 5 points ce que ça donne géométriquement parlant.
avec, pour tout
Reste à voir si on peut (plus ou moins) interpréter géométriquement le résultat en terme de surface de différents triangles. Il y en a des tas qui apparaissent et la façon de mener les calculs çi dessus en privilégiant l'origine
Je vais regarder avec 5 points ce que ça donne géométriquement parlant.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :