Bonjour a tous,
Je suis nouveau et je m'intéresse au programme de MPSI.
Je me posais la question suivante :
Soient 2 assertions A et B :
L'assertion non(A ou B) est elle identique à non A ou non B ? De même pour un cas de conjonction.
Merci beaucoup,
Bonsoir.
Logique
8 messages
- Page 1 sur 1
Non, bien sûr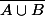
 et vice et versa.
et vice et versa.
Il faux utiliser les tables de vérité: lien
https://www.google.fr/search?q=Tables+de+v%C3%A9rit%C3%A9&rlz=1C1CHIK_frFR546FR549&espv=2&biw=1366&bih=643&tbm=isch&tbo=u&source=univ&sa=X&ei=YZlqVaumBoPfU7CXgeAE&ved=0CCcQsAQ&dpr=1
Il faux utiliser les tables de vérité: lien
https://www.google.fr/search?q=Tables+de+v%C3%A9rit%C3%A9&rlz=1C1CHIK_frFR546FR549&espv=2&biw=1366&bih=643&tbm=isch&tbo=u&source=univ&sa=X&ei=YZlqVaumBoPfU7CXgeAE&ved=0CCcQsAQ&dpr=1
Bonjour Beber59,
Ce que t'a dit Paquito est un des énoncés des Lois de De Morgan, tu peux aussi voir de ce côté là si la logique t'intéresse.. :lol3:
\Longleftrightarrow\neg P\vee\neg Q)
\Longleftrightarrow\neg P\wedge\neg Q)
Loi de De Morgan => Lien
Ce que t'a dit Paquito est un des énoncés des Lois de De Morgan, tu peux aussi voir de ce côté là si la logique t'intéresse.. :lol3:
Loi de De Morgan => Lien
Bonjour a vous, déjà merci d'avoir pris la peine de répondre !
En fait, j'ai compris mon erreur je pense.
Zygomatique : il n'a mangé ni poulet, ni steak je pense ? Donc on retrouve bien que non(A u B) <=> nonA n nonB
Je pense avoir compris avec les tables. Mais quand vous voyez par exemple que p=>q est équivalent a nonp ou q, c'est intuitif pour vous ? Parce que en passant par les tables on le retrouve certes, mais je trouve que c'est dur de s'imaginer cette assertion, vous avez un exemple ?
Merci beaucoup! Bonne journée
En fait, j'ai compris mon erreur je pense.
Zygomatique : il n'a mangé ni poulet, ni steak je pense ? Donc on retrouve bien que non(A u B) <=> nonA n nonB
Je pense avoir compris avec les tables. Mais quand vous voyez par exemple que p=>q est équivalent a nonp ou q, c'est intuitif pour vous ? Parce que en passant par les tables on le retrouve certes, mais je trouve que c'est dur de s'imaginer cette assertion, vous avez un exemple ?
Merci beaucoup! Bonne journée
Bonjour,
Non pas tellement, mais c'est justement pour rendre ((non p) ou q) plus intuitif qu'on le symbolise par une flèche (p => q).
"si il pleut (A) alors je prends mon parapluie (B)" soit "A => B" : il y a deux façon que la chose se réalise :
- soit il ne pleut pas (non A), dans ce cas peu importe que j'aie mon parapluie ou pas, ça sera vrai ;
- soit j'ai mon parapluie (B), dans ce cas peu importe qu'il pleuve ou pas, ça sera vrai aussi.
donc (A => B) est équivalente à ((non A) ou B), la seule façon que (A => B) ne se réalise pas, c'est quand il pleut et que je me retrouve sans parapluie, soit (A et (non B)) qui est aussi non((non A) ou B).
Beber59 a écrit: Mais quand vous voyez par exemple que p=>q est équivalent a nonp ou q, c'est intuitif pour vous ?
Non pas tellement, mais c'est justement pour rendre ((non p) ou q) plus intuitif qu'on le symbolise par une flèche (p => q).
"si il pleut (A) alors je prends mon parapluie (B)" soit "A => B" : il y a deux façon que la chose se réalise :
- soit il ne pleut pas (non A), dans ce cas peu importe que j'aie mon parapluie ou pas, ça sera vrai ;
- soit j'ai mon parapluie (B), dans ce cas peu importe qu'il pleuve ou pas, ça sera vrai aussi.
donc (A => B) est équivalente à ((non A) ou B), la seule façon que (A => B) ne se réalise pas, c'est quand il pleut et que je me retrouve sans parapluie, soit (A et (non B)) qui est aussi non((non A) ou B).
p => q
P = "il pleut"
q = "la route est mouillée"
p => q = "si il pleut alors la route est mouillée"
non p ou q = " il ne pleut pas ou la route est mouillée"
qu'il pleuve ou non si la route est mouillée alors p => q et non p ou q sont vraies
ou :: l'une ou l'autre est vraie
=> :: la conclusion est vraie
si la route n'est pas mouillée alors non p ou q est fausse lorsque non p est fausse <=> p est vraie
mais si p est vraie alors q est vraie donc p => q est vraie
...
P = "il pleut"
q = "la route est mouillée"
p => q = "si il pleut alors la route est mouillée"
non p ou q = " il ne pleut pas ou la route est mouillée"
qu'il pleuve ou non si la route est mouillée alors p => q et non p ou q sont vraies
ou :: l'une ou l'autre est vraie
=> :: la conclusion est vraie
si la route n'est pas mouillée alors non p ou q est fausse lorsque non p est fausse <=> p est vraie
mais si p est vraie alors q est vraie donc p => q est vraie
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Il y a tout d'abord un truc à bien comprendre, c'est que les mots utilisés en mathématique on un sens "carré-carré" qui ne correspond pas systématiquement avec le sens "usuel" en français.Beber59 a écrit:Je pense avoir compris avec les tables. Mais quand vous voyez par exemple que p=>q est équivalent a nonp ou q, c'est intuitif pour vous ? Parce que en passant par les tables on le retrouve certes, mais je trouve que c'est dur de s'imaginer cette assertion, vous avez un exemple ?
Exemple 1 : Le "ou" mathématique est défini comme voulant dire systématiquement l'un ou l'autre ou les deux.
Ce n'est très clairement pas le cas du "ou" de "fromage ou dessert" que l'on trouve dans les menus des resto.
Par contre un "tarif réduit pour les titulaires d'une carte d'étudiant ou d'invalidité" va offrir un tarif réduit à la personne étudiante ET invalide.
Exemple 2 : Le => (implique mathématique) n'a pas le même sens que le sens du "si... alors..." du langage courant qui, presque toujours, correspond à une causalité : "Cause" => "Effet" avec évidement la cause qui précède l'effet dans le temps.
Pour reprendre la notion de contraposée mathématiques, si tu dit à quelqu'un "s'il pleut alors je prend mon parapluie" tout va bien, mais si tu dit "si je ne prend pas mon parapluie alors il ne pleut pas", la plupart des gens vont penser que tu "fait la pluie et le beau temps", c'est à dire que c'est toi, en ne prenant pas ton parapluie (=cause) qui va provoquer qu'il ne pleuvra pas (=effet=conséquence de la cause).
En math, il n'y a pas de temps, donc la cause ne précède pas l'effet : tout se passe "en même temps".
Il ressort de ces deux exemples qu'il faut pas mal se méfier des exemples de la logique mathématique appliquée "à la vie de tout les jours" : avec certains exemples, ça marche pas mal, mais avec d'autres, c'est n'importe quoi.
Concernant la contraposée, perso, je préfère donner principalement des exemples mathématiques très simples :
- On sait que, pour une fonction R->R donnée, si f est dérivable sur R alors f est continue sur R et cela équivaut à dire que, si f n'est pas continue sur R alors elle n'est pas dérivable sur R.
- La contraposée de (si x>2 alors x>1) (proposition vraie) est (si x=b alors x>=a) (idem)
EDIT : et concernant le coté "intuitif", ben c'est comme... absolument tout... c'est à dire qu'à force de pratiquer, ça devient complètement intuitif.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
