Valeurs propres

[marocpalestine]

bonjour quelle difference svp entre valeur propore simple et valeur propre double svp

[Ben314]

Salut,
A mon avis, ça doit signifier que lambda est racine simple [respectivement double] du polynôme caractéristique.

Mais je trouve ça bien ambigüe vu que ça pourrait vouloir dire "racine simple [ou double] du polynôme minimal".
Ca explique que, perso., j'utiliserais pas cette expression, (surtout que "racine simple du polynôme caractéristique" c'est pas archi plus long à écrire que "valeur propre simple")

[marocpalestine]

Ah merci et tu sais c'est les les sous espace propre stp

[Ben314]

Tu as pas de cours ni d'internet ?
Si est une valeur propre de l'endomorphisme alors le sous espace propre associé à , c'est le noyau de , c'est à dire l'ensemble des vecteurs tels que

[Skullkid]

Bonjour, à ma connaissance il y a 3 interprétations possibles à la multiplicité d'une valeur propre :

- Multiplicité en tant que racine du polynôme caractéristique, parfois nommée "multiplicité algébrique".
- Dimension du sous-espace propre associé, parfois nommée "multiplicité géométrique".
- Multiplicité en tant que racine du polynôme minimal, je crois pas qu'il y ait de nom spécial pour cette interprétation-là.

Ces 3 multiplicités peuvent toutes être différentes donc comme l'a dit Ben314 il vaut mieux préciser dans quel cadre on se place pour éviter les ambiguïtés.

[paquito]

Déjà, ça dépend si on travaille dans ou dans; dans , le polynôme caractèrisque est sous la forme et l'ordre de multiplicité de 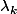est le nombre de fois oùapparaît . dans ,on peut très bien avoir et il n'y a pas de valeur propre et la matrice associée n'est même pas triangulable;
si on prend , on a mais le s.ev. associé à 1 a pour dimension 0, tandis que le s.ev. associé à 2 a pour dimension 1 et le polynnôme minimal est P(x). On peut trouver plein d'autres exemples.