bonjour j ai un dm a rendre ce mardi et je n'arrive pas du tout à faire cet exercice
Dans un plan, muni dun repère orthonormal (O i j) on considère les points : A(2 ; 1) , B(5 ; 7)
, C(3 ; -1) et D(5 ; 5) .
On note ;) lensemble des points M(x ; y) du plan tels que AM ;) AB= 27 et ;) le cercle de
diamètre [CD].
1. a. Déterminer une équation cartésienne de ;) et ;).
b. Vérifier que H(-1 ; 7) est un point de ;) et que E(1 ; 1) est un point de ;).
c. Construire ;) et ;).
2. a. Résoudre le système (S)
x+2y-13=0
x²+y²-8x+4y+10=0
b. Que peut-on en déduire ?
3. Déterminer léquation réduite de la tangente D à ;) au point E puis la tracer.
4. Déterminer les coordonnées des points dintersection de ;) avec les axes du repère.
Geometrie
8 messages
- Page 1 sur 1
Salut !
1. a) Indication donnée par mathelot.
1.b) si et seulement si ses coordonnées vérifient l'équation cartésienne de
si et seulement si ses coordonnées vérifient l'équation cartésienne de  ;
;
 si et seulement si ses coordonnées vérifient l'équation cartésienne de
si et seulement si ses coordonnées vérifient l'équation cartésienne de  .
.
1.c) est une droite dont on a déterminer l'équation cartésienne, on peut donc lui trouver un vecteur directeur
est une droite dont on a déterminer l'équation cartésienne, on peut donc lui trouver un vecteur directeur 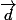 . Enfin, sachant que
. Enfin, sachant que  , tu en peux en déduire l'emplacement de la droite recherchée.
, tu en peux en déduire l'emplacement de la droite recherchée.
Réécris l'équation de sous la forme
sous la forme ^2+(y-b)^2=r^2) où
où 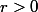 et
et ) est un couple de réels. Alors le point
est un couple de réels. Alors le point  de coordonnées
de coordonnées ) est le centre du cercle
est le centre du cercle  et de plus
et de plus  donc tu peux facilement trouver son rayon
donc tu peux facilement trouver son rayon  . Connaissant la position de
. Connaissant la position de  et la valeur de
et la valeur de  , tu pourras tracer ton cercle.
, tu pourras tracer ton cercle.
2.a) A partir de l'équation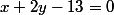 exprime
exprime  en fonction de
en fonction de  , puis remplace l'expression de
, puis remplace l'expression de  obtenue dans la seconde équation
obtenue dans la seconde équation  . Montre donc que résoudre
. Montre donc que résoudre ) revient à résoudre :
revient à résoudre :
[CENTER]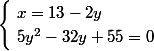 [/CENTER]
[/CENTER]
L'équation ne contient qu'une seule des deux variables recherchée, résous-la.
ne contient qu'une seule des deux variables recherchée, résous-la.
b) Résoudre) revient à déterminer l'ensemble des points
revient à déterminer l'ensemble des points  vérifiant
vérifiant  .
.
3. Indication donnée par mathelot.
4. Je te donne le principe dans le cas où l'on cherche les coordonnées des points dintersection de avec l'axe des abscisses.
avec l'axe des abscisses.
Soit) les coordonnées d'un point
les coordonnées d'un point  quelconque du plan.
quelconque du plan.  est un point d'intersection de
est un point d'intersection de  est l'axe des abscisses si et seulement si ses coordonnées vérifient l'équation de
est l'axe des abscisses si et seulement si ses coordonnées vérifient l'équation de  et
et  (un point est situé sur l'axe des abscisses si et seulement si son ordonnée est nulle). En conséquence, si un point
(un point est situé sur l'axe des abscisses si et seulement si son ordonnée est nulle). En conséquence, si un point  appartient à l'intersection de
appartient à l'intersection de  et de l'axe des abscisse, ses coordonnées sont de la forme
et de l'axe des abscisse, ses coordonnées sont de la forme ) . En conclusion, les abscisses des points dintersection de
. En conclusion, les abscisses des points dintersection de  avec l'axe des abscisses sont solutions de l'équation
avec l'axe des abscisses sont solutions de l'équation  .
.
:+++:
1. a) Indication donnée par mathelot.
1.b)
1.c)
Réécris l'équation de
2.a) A partir de l'équation
[CENTER]
L'équation
b) Résoudre
3. Indication donnée par mathelot.
4. Je te donne le principe dans le cas où l'on cherche les coordonnées des points dintersection de
Soit
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:Salut !
1. a) Indication donnée par mathelot.
1.b)si et seulement si ses coordonnées vérifient l'équation cartésienne de
;
si et seulement si ses coordonnées vérifient l'équation cartésienne de
.
1.c)est une droite dont on a déterminer l'équation cartésienne, on peut donc lui trouver un vecteur directeur
. Enfin, sachant que
, tu en peux en déduire l'emplacement de la droite recherchée.
Réécris l'équation desous la forme
où
et
est un couple de réels. Alors le point
de coordonnées
est le centre du cercle
et de plus
donc tu peux facilement trouver son rayon
. Connaissant la position de
et la valeur de
, tu pourras tracer ton cercle.
2.a) A partir de l'équationexprime
en fonction de
, puis remplace l'expression de
obtenue dans la seconde équation
. Montre donc que résoudre
revient à résoudre :
[CENTER][/CENTER]
L'équationne contient qu'une seule des deux variables recherchée, résous-la.
b) Résoudrerevient à déterminer l'ensemble des points
vérifiant
.
3. Indication donnée par mathelot.
4. Je te donne le principe dans le cas où l'on cherche les coordonnées des points dintersection deavec l'axe des abscisses.
Soitles coordonnées d'un point
quelconque du plan.
est un point d'intersection de
est l'axe des abscisses si et seulement si ses coordonnées vérifient l'équation de
et
(un point est situé sur l'axe des abscisses si et seulement si son ordonnée est nulle). En conséquence, si un point
appartient à l'intersection de
et de l'axe des abscisse, ses coordonnées sont de la forme
. En conclusion, les abscisses des points dintersection de
avec l'axe des abscisses sont solutions de l'équation
.
:+++:
merci mais je n'arrive pas à faire la figure svp aidez moi je ss en larmes
dimouche972 a écrit:Dans un plan, muni dun repère orthonormal, on considère les points :
,
,
et
. On note
lensemble des points
du plan tels que
et
le cercle de diamètre
.
1.a) Déterminer une équation cartésienne deet
.
1.b) Vérifier queest un point de
et que
est un point de
.
1.c) Construireet
.
La construction est demandée en troisième question : d'après ce qui a été dit précédemment, as-tu répondu au deux premières questions ? As-tu trouvé équation cartésienne de
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 89 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

